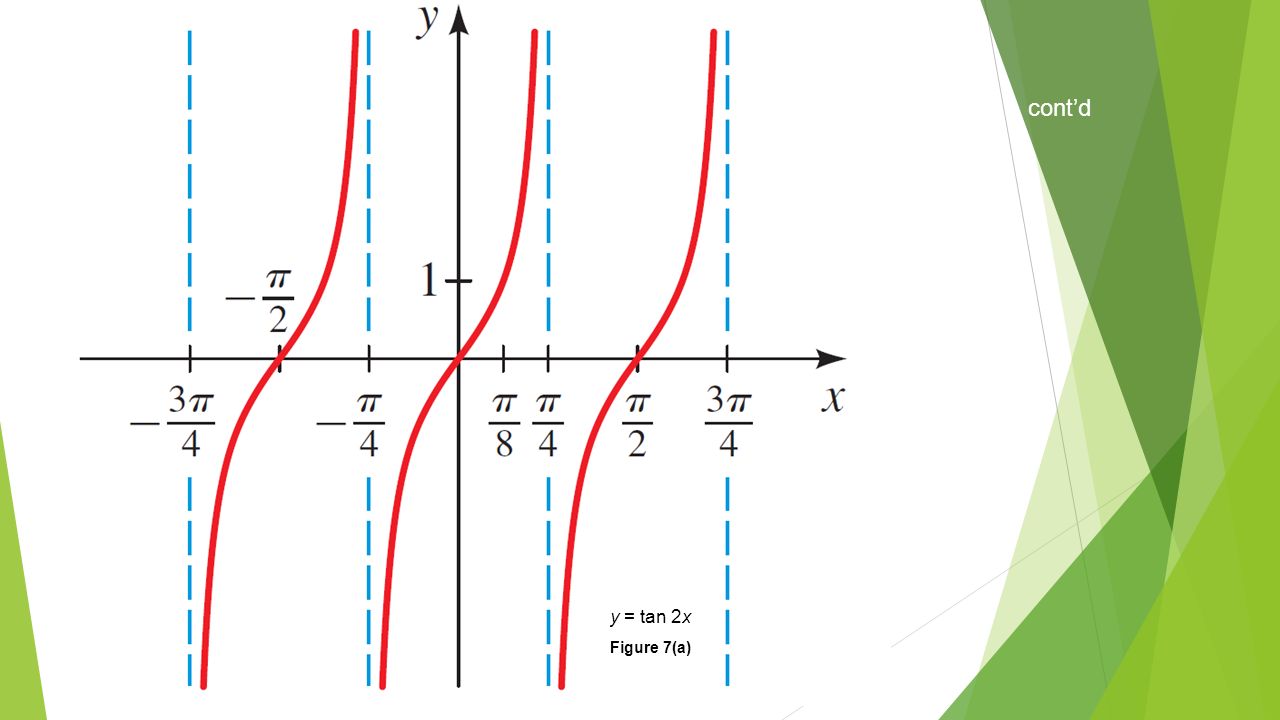
TAN to 90 degrees (PI/2 Radians) is 1/0, which is undefined, so you can't graph a result that's not there You can get as close as you want to 90 degrees, as long as you don't land on it Example TAN () ≈ 572,957,795,131 TAN (90) = 1/0 = UNDEFINEDMultiply 2 2 by 2 2 x = π 4 x = π 4 x = π 4 x = π 4 x = π 4 x = π 4 The basic period for y = tan ( 2 x) y = tan ( 2 x) will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a tan(x) = 1 everywhere sin(x) = cos(x) This is at pi/4 and every pi after that Draw a few of those It is zero everywhere sin(x) = 0 That's x = 0 and every pi after that Draw a few of those You should be seeing the shape of the thing Sketch a few periods y = 2tan(x) This is just a little vertical stretching Start with the graph
Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf
How to graph tan
How to graph tan-The graphs of trigonometric functions have the domain value of θ represented on the horizontal xaxis and the range value represented along the vertical yaxis cos(2x) = cos 2 (x)–sin 2 (x) = (1tan 2 x)/(1tan 2 x) cos(2x) = 2cos 2 (x)−1 = 1–2sin 2 (x which by substituting the value of x in degrees gives the slope value ofIf you can remember the graphs of the sine and cosine functions, you can use the identity above (that you need to learn anyway!) to make sure you get your asymptotes and xintercepts in the right places when graphing the tangent function At x = 0 degrees, sin x = 0 and cos x = 1 Tan x must be 0 (0 / 1) At x = 90 degrees, sin x = 1 and cos x = 0
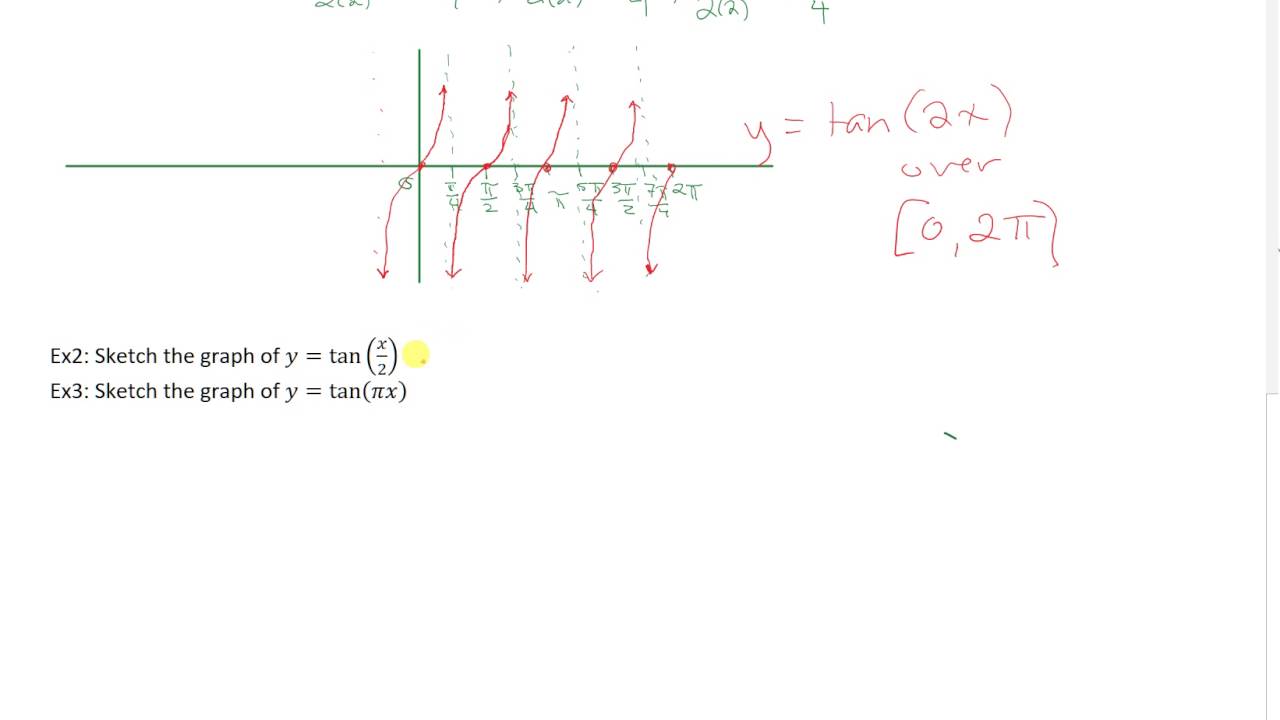



Sketching Y Tan 2x And Y Tan X 2 Youtube
The question is "What is the closest graph of math\tan(\sin x), x>0?/math The graph of math\tan(\sin x)/math is given below This similar to (but not exactly) a triangular wave The maximum and minimum values are math\tan(1)/math and0 There is no direct way of calculating a closed form solution for x from the equation tan x − 2 x = C for an arbitrary value of C That said, however, in your particular case, plotting both tan x and 2 x will quickly show you there are more solutionsThe vertical asymptotes for y = 2 tan ( x) y = 2 tan ( x) occur at − π 2 π 2, π 2 π 2 , and every π n π n, where n n is an integer π n π n There are only vertical asymptotes for tangent and cotangent functions Vertical Asymptotes x = π 2 π n x = π 2 π n
Proportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengthsFrom what I know about the graph of the tangent, I know that the tangent will equal 1 at 45° after every 180° These solutions for tan( x /2) are at 0° 45°, 180° 45°, 360° 45° , and so forth Answers #1 0 Since the result is 2, it must mean that the opposite side divided by the djacent side equals 2 This only occurs whens the oppostie side is twice the adjacent side Therefore it must be at an angle of 30 degrees If you draw the triangle this can be verified Guest
We know that any trignometic fn of 2n (Pi) or minus (angle theta) = or minus the angle theta Pi radians = 360 degrees Therefore to (780)degrees add the nearest positive number of revolutions namely two revoultions in this problem that is add 2X (360)=7 degrees Then (780) 7 = (60)degreesSin 30° = 1/2 & Cos 30° = √3/2 ∴ Tan 30° = (1/2) / (√3/2) Tan 30° = 1/√3 Hence, the value of Tan 30 degrees is 1/√3 We can also find the value of tan 0, tan 45, tan 60 and tan 90 in the same manner Tan 0 = sin 0/cos 0 = 0/1 = 0 Tan 45 = sin 45/cos 45 = (1/√2)/ (1/√2) = 1 Tan 60 = sin 60/cos 60 = (√3/2)/ (½) = √3Answer to Find the period y = tan(2x pi/2) Graph the function By signing up, you'll get thousands of stepbystep solutions to your homework



How Do You Graph Y Tan3x Class 12 Maths Cbse



2
Tan(x) degrees radians90°π/2 not defined60°π/°π/4130°π/ 0° 0 0 30° π/6 45° π/4 1 60° π/3 90° π/2 not #y=tan(x60)# Amplitude ( see below) period #= pi/c# in this case we are using degrees so period #=180/1=180^@# Phase shift #=c/b=60/1=60^@# This is the same as the graph of y = tan(x) translated 60 degrees in the negative x direction Vertical shift #= d = 0# ( no vertical shift ) Amplitude can not be measured for the tangent function Assuming you know what ), the function is squished along the xaxis by a So, a= represents all the xvalues being doubled So if for a function f(x), f(2)=5 and f(4)=12, with f(x/2) f(4)=5 So, y=tan(x/2) would be y=tanx but each value of x would be doubled y=tanx graph{tanx 10, 10, 5, 5} y=tan(x/2)# graph{tan




C3 3 Trigonometry 1



h Graphing Tangent Test Algebra Ii Quiz Quizizz
Type in any function derivative to get the solution, steps and graph This website uses cookies to ensure you get the best experience Decimal to Fraction Fraction to Decimal Radians to Degrees Degrees to Radians Hexadecimal Scientific (tan^{2}x\right) en Related Symbolab blog posts High School Math Solutions – Derivative Calculator Sketch the graph of y = 2 sinx 1 and state its rangeLeave your answer as "a 7 Sketch the graph of y = 3 cos2x and state its rangeLeave your answer as "a 8 Sketch the graphs y=4sin 2x and y = 2cosx 1 for 0I put tan 2x into an online graphic calculator, and it came up with a straight line of negative gradient going through the origin You just has the scale set wrong or something It'd be best to have it at, say, 360 degrees to 360 degrees on the x axis and 10 to 10 on the y axis?



Solved Graph One Complete Cycle For The Following Label The Axes Accurately And Identify The Period For The Graph Course Hero



Draw The Graph Of Y Tan 3x
Arctan Graph ( x) The feature f(x) = arctan( x) graphed for a single period Evidence of the Derivative Rule Since arctangent ways inverse tangent, we understand that arctangent is the inverse feature of a tangent Consequently, we may confirm the byproduct of Arctan ( x) by associating it as an inverted function of deviationGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! explain what each part would represent in a graph of this function Samuel tan(2x1) = tan(2(x 1/2)) since tan(kx) has period π/k, this has period π/2 Jan 32 degrees Feb 35 degrees Mar 44 degrees Apr 53 degrees May 63 degrees June 73 degrees July 77 degrees Aug 76 degrees Sept 69 degrees Oct 57 degrees Nov 47 Alg 2 trig



Www Sheffield Ac Uk Polopoly Fs 1 4656 File 19 Trigonometric Equations Pdf



Http Chesshir Weebly Com Uploads 8 6 7 9 4 5 4 7 Pdf
The diagram shows a graph of y = tan x for 0˚ ≤ x ≤ 360˚, determine the values of p, q and r Solution We know that for a tangent graph, tan θ = 1 when θ= 45˚ and 225˚ So, b = 45˚ We know that for a tangent graph, tan θ = 0 when θ= 0˚, 180˚ and 360˚ So, c = 180˚ Graphing the Tangent FunctionY=tan 2x for the lower values of x probably does look something How to graph these two circular functions Tan and Cot cycle in 180 degrees not in 360 degrees Some of my favorite tools https//wwwamazoncom/shop/colfa




Trig 2 Caldervale High School
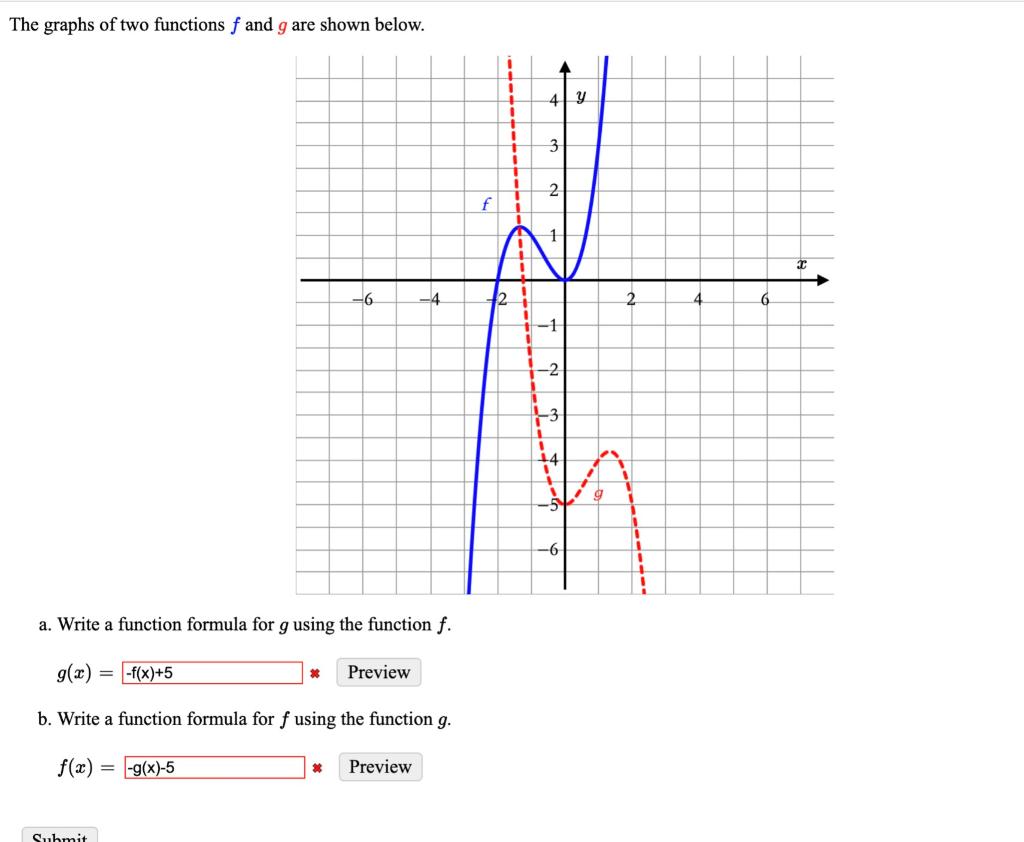



Precalculus Archive March 06 21 Chegg Com
Use the definition of tangent For any two differentiable functions, the derivative of the quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the denominator squared The derivative of sin (x) is cos (x), and the derivative of cos (x) isTo calculate tan (45) degrees of a right angled triangle, we use the following equation where angle is 45 Tan(angle) = Opposite/Adjacent Tan 45 degrees is simply the ratio of the side opposite of the angle to the side adjacent to the angle As long as the angle stays at 45 degrees, the ratio does not change and tan 45 degrees is a fixed numberWe draw a graph of tanu over this interval as shown in Figure 4 90 180 360 5401 135 315 495 1 45 tan€ u u o o o o Figure 4 A graph of tanu We know from the Table on page 2 that an angle whose tangent is 1 is 45 , so using the symmetry in the graph we can find the angles which have a tangent equal to −1 The first will be the same
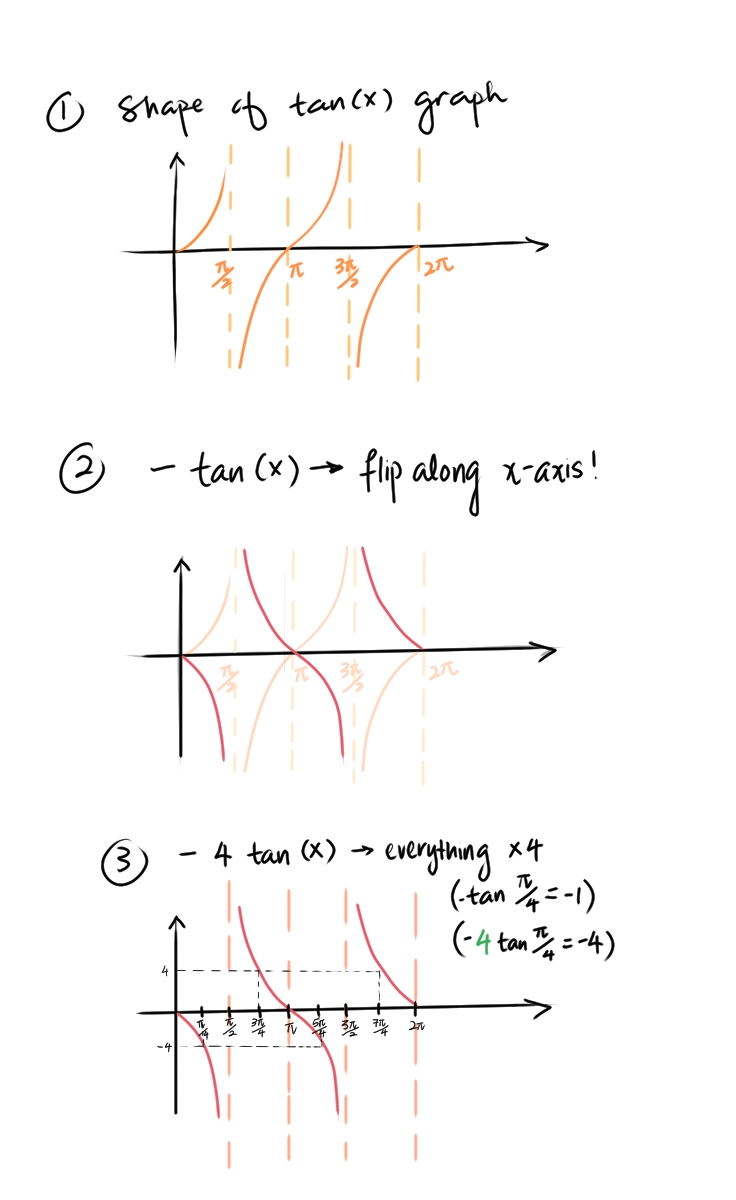



How Do You Graph Y 4 Tan X Socratic
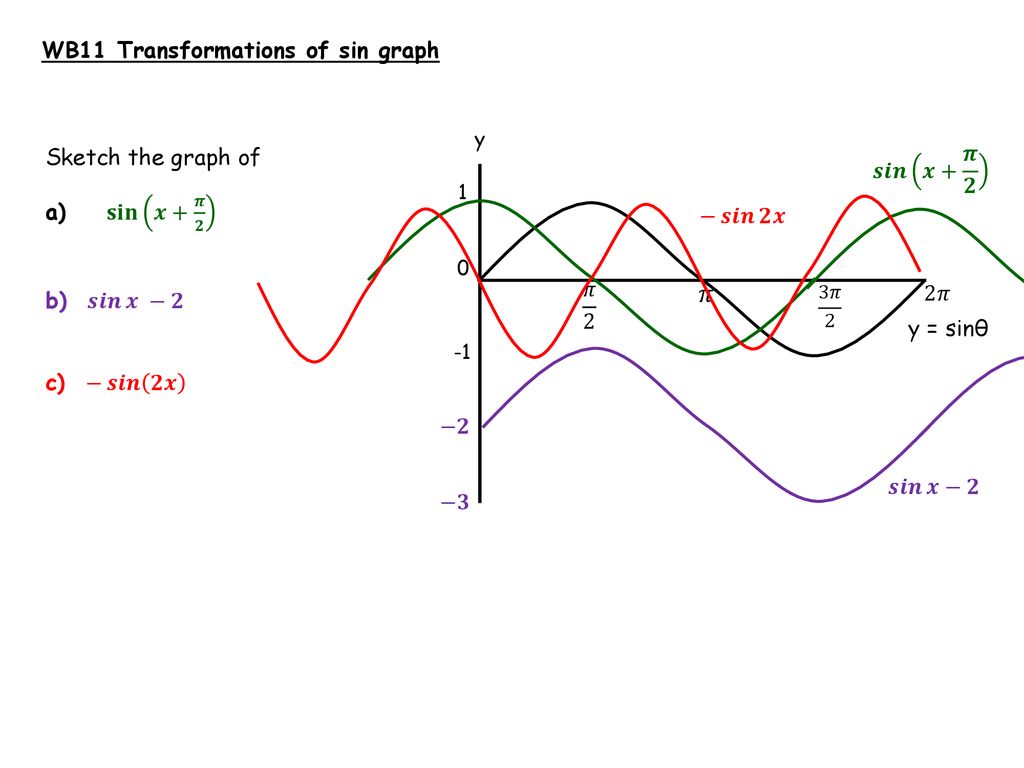



Trig Graphs And Equations Ppt Download
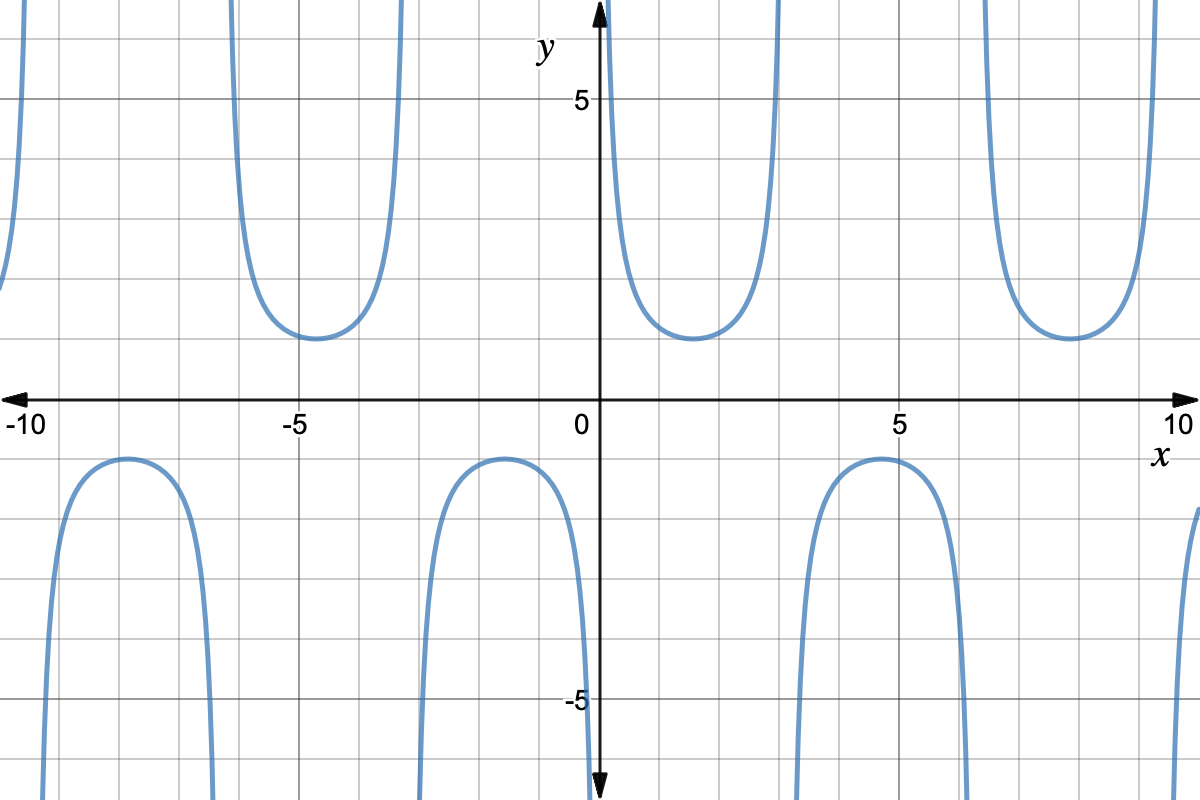
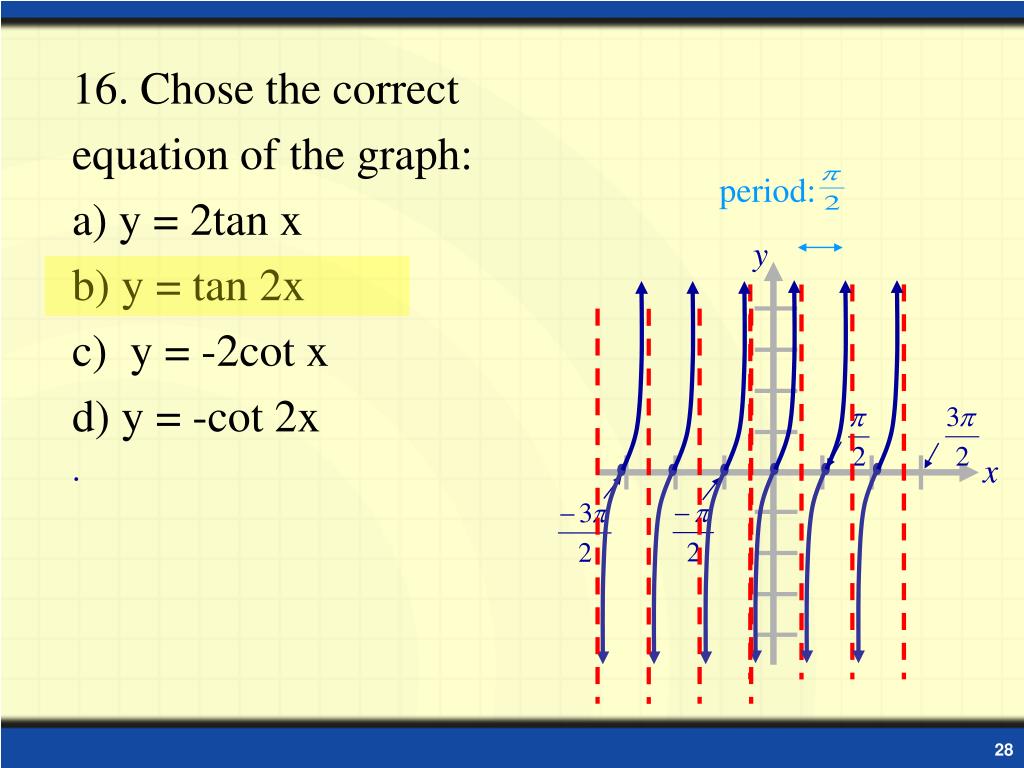
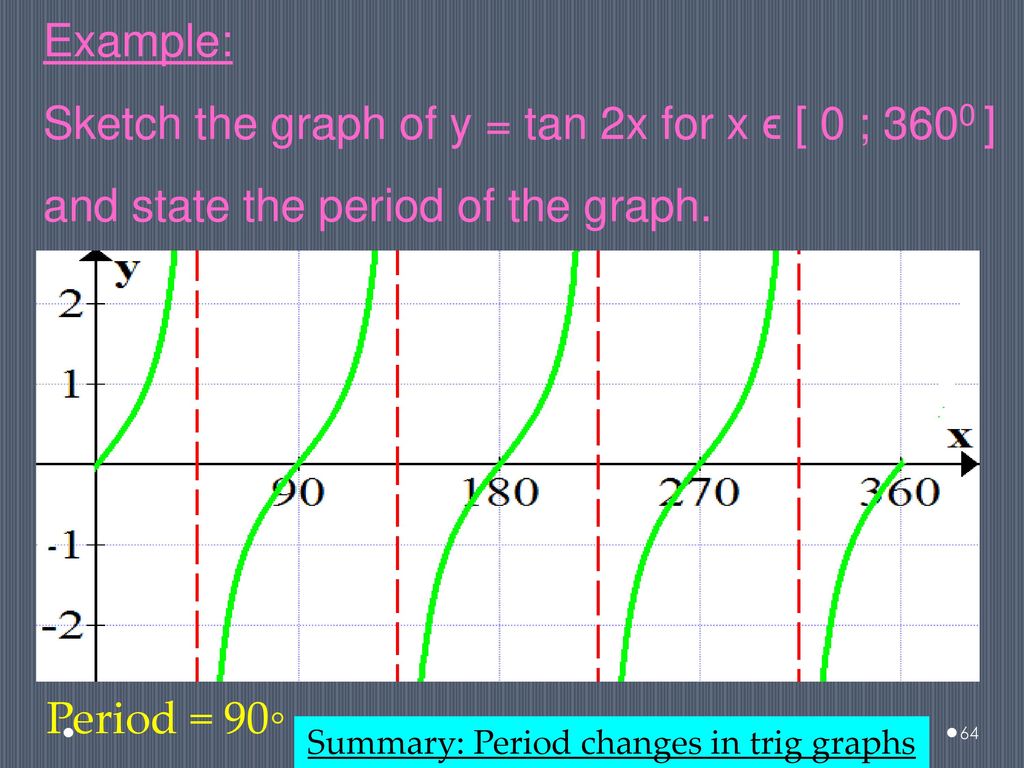
Graph of tangent and cotangent Which graph is sketched in the given image Which graph is sketched in the given image is an odd function and its graph is symmetric with respect the origin is an even function and its graph is symmetric with respect the origin Which graph is sketched in the given image Which graph is sketched in the givenTan graph Loading Tan graph Tan graph Log InorSign Up y = a tan b x − h k 1 a = 1That is not 360 degrees as you might suppose tan x repeats every 180 degrees it's normal period is therefore 180 degrees the period is determined by the normal period divided by the frequency that would make tan(2x) period equal to 180/2 = 90 degrees below is a graph of tan(x) those vertical lines are at 90 degrees (pi/2) and 270 degrees (3pi/2) that's a period of 180 degrees (pi)
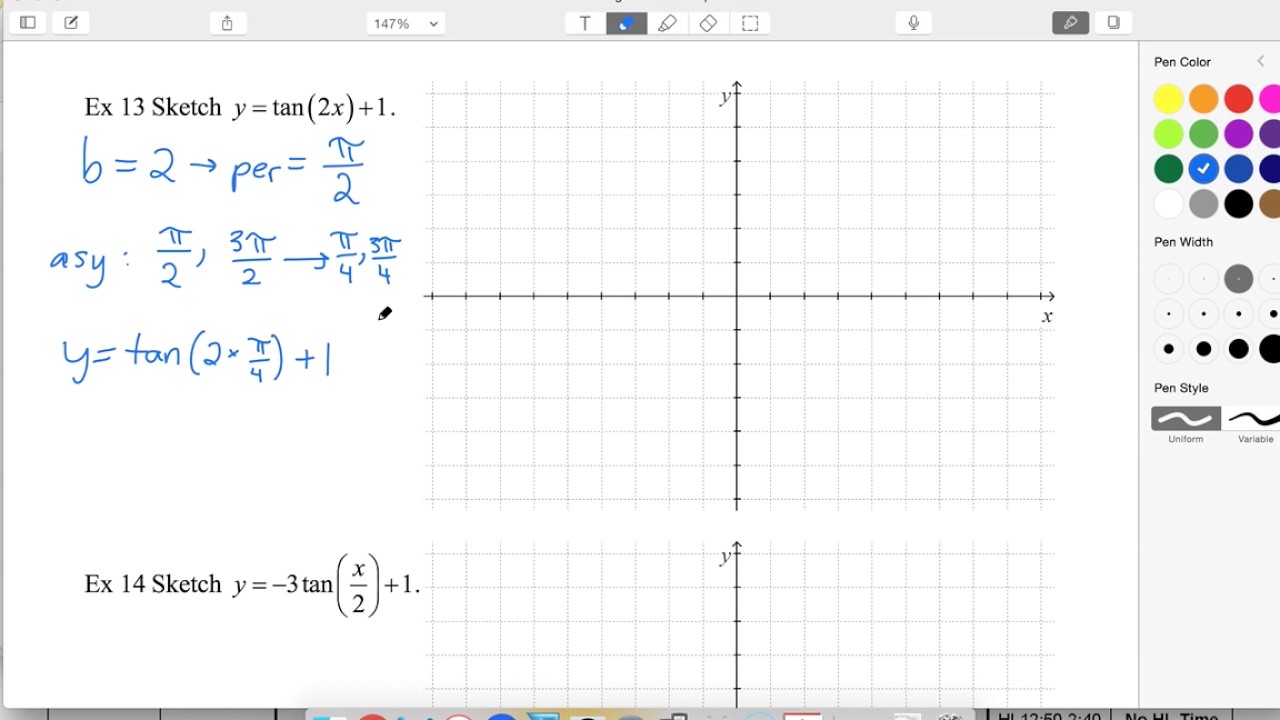



01 Ex13 Sketch Y Tan 2x 1 Youtube



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf
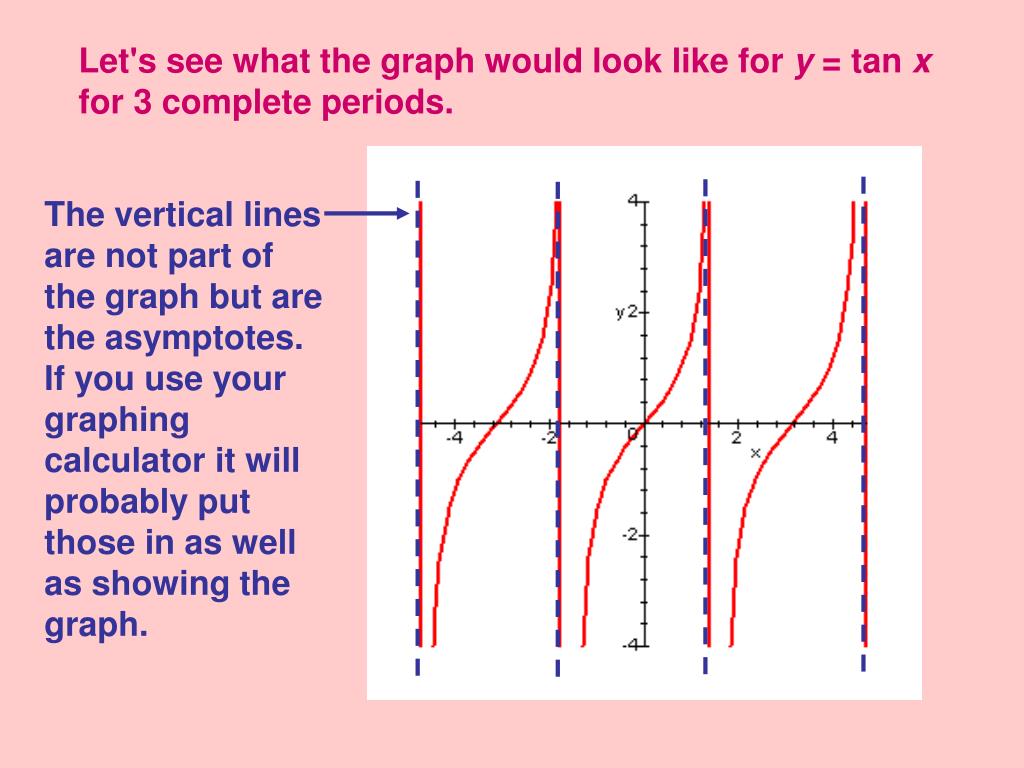
This result is so beautiful and make me interested in the equation $\tan x= \tan2x\tan3x\tan4x$, but I have difficulty in solving it By plotting the graph, I can see that the solution is $180n^\circ$ or $60n^\circ\pm10^\circ$ My questions are (\cos3x\cos 4x 4\cos^2 x\sin 3x\sin 2x)=0$$ Further factorize with $\cos 3x = \cos xAnalyzing the Graph of y = tan x We will begin with the graph of the tangent function, plotting points as we did for the sine and cosine functions Recall that tanx = sinx cosx t a n x = s i n x c o s x The period of the tangent function is π π because the graph repeats itself on Answer sin ( − π 12) = √ 3 − 1 2 √ 2 16) cos( − 5 π 12) In exercises 17 22, consider triangle ABC, a right triangle with a right angle at C a Find the missing side of the triangle b Find the six trigonometric function values for the angle at




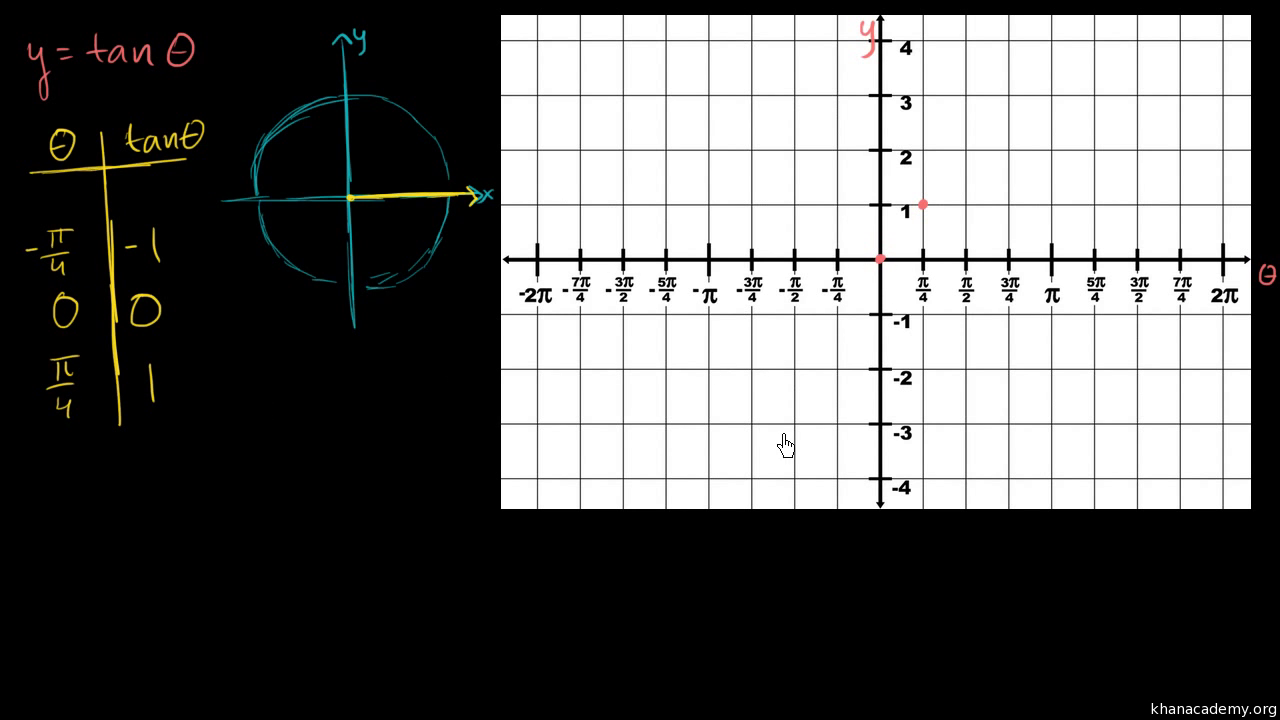
Graph Of Y Tan X Video Trigonometry Khan Academy



Http Www Brooklyn Cuny Edu Web Aca Naturalsciences Math Study Guide Final Exam Math 1011 1012 Pdf
The line \ (y = 075\) crosses the graph of \ (y = \cos {x}\) four times in the interval \ (360^\circ \leq x \leq 360^\circ\) so there are four solutions There is a line of symmetry at \ (x = 0The red graph, again, is the standard y = tan x graph The red graph has a phase shift applied to it The only difference between the equations of the two graphs is the value of C is 45 Given an equation y = A tan B (x C) , the value of C dictates the phase shift Note that the standard equation has a negative sign Right side 12tan^2 (x) from the trig identity sec^2x tan^2x = 1 sec^2x tan^2x 2tan^2x = 12tan^2x simp lying this sec^2x tan^2x So right side now matches left side 👍
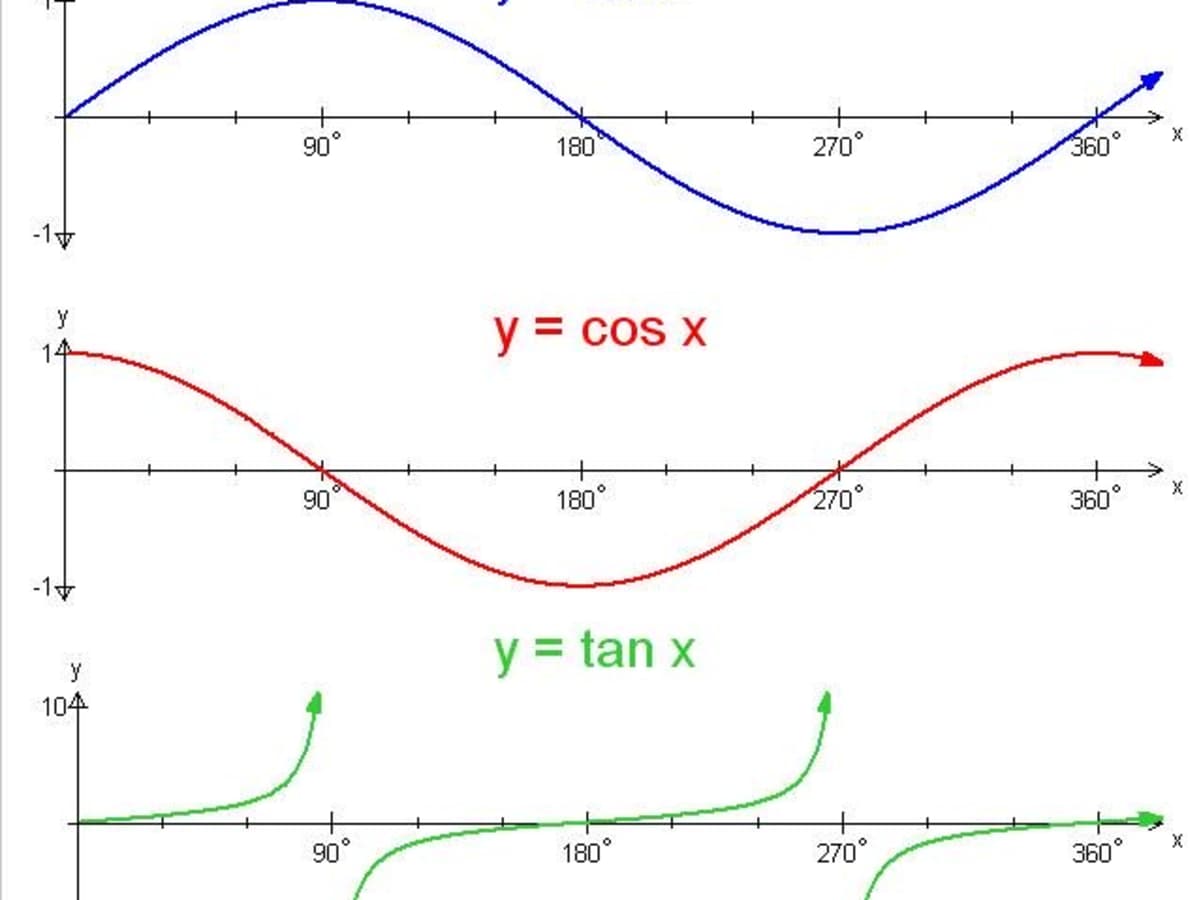



Trigonometry Graphing The Sine Cosine And Tangent Functions Owlcation



Trigonometry Reciprocal Identities Expii
Graph the function {eq}y = \frac{2 sin(2x)}{cos x 3 cos(2x)} {/eq} Graphs Graphing trigonometric functions is a great way of finding the roots of the trigonometric functionTan^2(x) = 3 , tanx = `sqrt(3)` , x = tan^1(`sqrt(3)` ) = 60 degrees thus x = pi/3Hence, the general solutions of the equation `tan^x=3tanx` are `x_1= 180k` degrees and `x_2= 716 180k` degrees



Ppt Graphs Of Trigonometric Functions Powerpoint Presentation Free Download Id



5 Functions Straight Lines Parabolas Hyperbolas Exponential Graphs Ppt Download
Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomes \(tan(aa) =\frac{ tan a tan a }{1 tan a tana}\) \(Tan 2a =\frac{2tan a}{1tan^{2}a} \) Practice Example for tan 2 theta QuestionSubsection The Tangent Function The transformations of shifting and stretching can be applied to the tangent function as well The graph of \(y=\tan x\) does not have an amplitude, but we can see any vertical stretch by comparing the function values at the guidepoints Example 712 Graph \(y=13\tan 2x\text{}\)To supply an angle to TAN in degrees, multiply the angle by PI()/180 or use the RADIANS function to convert to radians For example, to get the TAN of 60 degrees, you can use either formula below = TAN ( 60 * PI () / 180 ) = TAN ( RADIANS ( 60 ))



How Can We Draw The Graph Of Tan X 2 Its Tan X Square And Not Tan Square X Quora




Ppt Graphs Of Other Trigonometric Functions Powerpoint Presentation Free Download Id
Le's start from 1/x here is a graph first understand what 1/x does when x goes away from zero 1/x foes to zero but when x goes near zero 1/x increase or decrease rapidly depending on the sign now come to tan(x) it is pretty straight forewordGraphing Tangent Function The trigonometric ratios can also be considered as functions of a variable which is the measure of an angle This angle measure can either be given in degrees or radians Here, we will use radians Since, tan(x) = sin ( x) cos ( x) the tangent function is undefined when cos(x) = 0



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 4 Pdf



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 4 Pdf
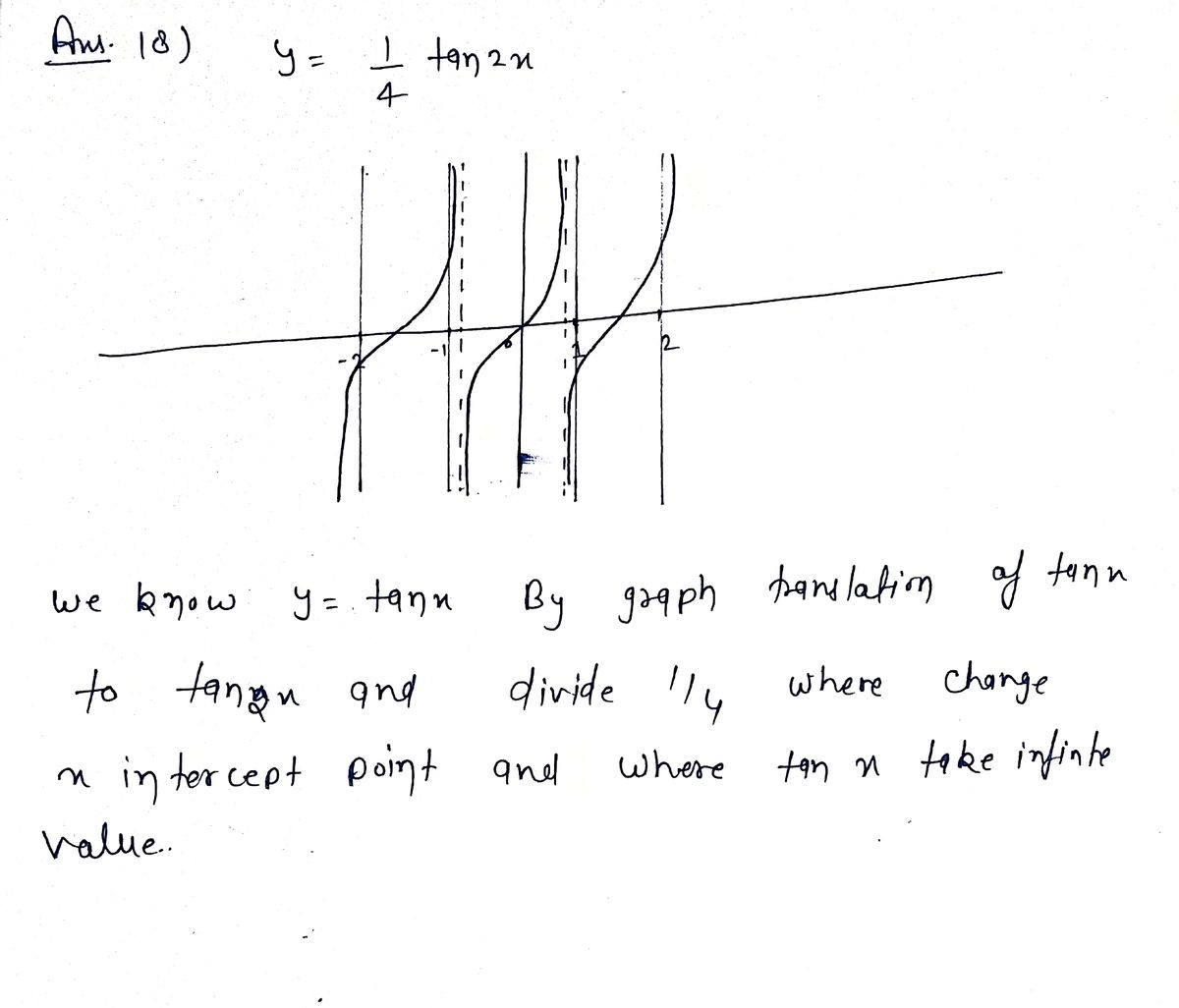



Answered Graph The Function 18 Y Tan 2x Bartleby
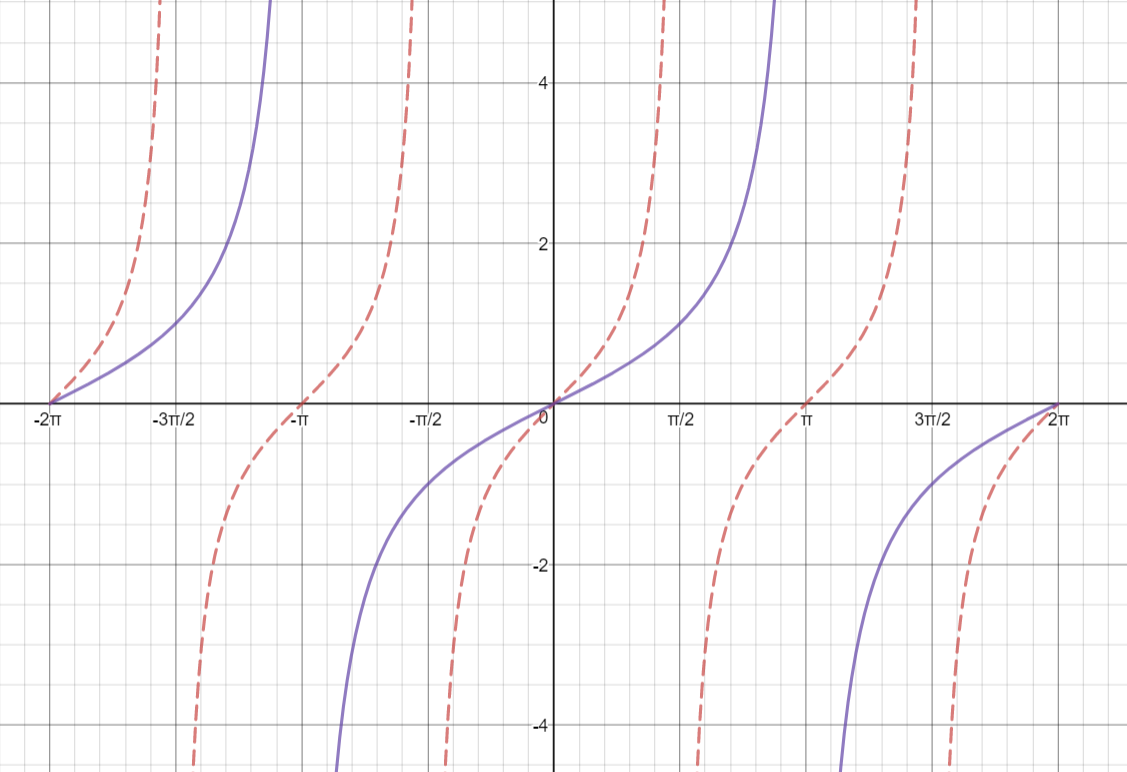



How Do You Graph Y Tan 1 2 X Socratic
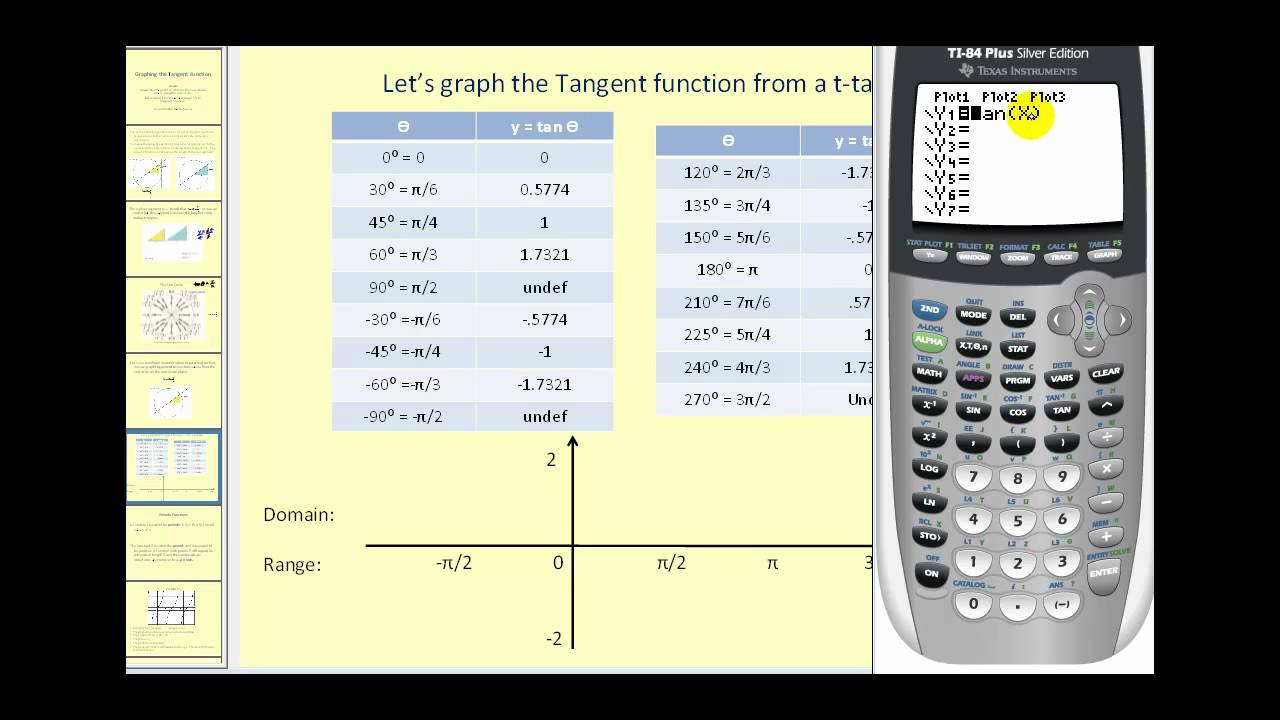



Tangent Graphs Worked Solutions Examples Videos



Graphing Trig Functions Geogebra



Tan2x ただの悪魔の画像



1




Ex Solve Tan X A On 0 2pi With A Calculator Negative A Youtube



Ppt Graphs Of Other Trig Functions Powerpoint Presentation Free Download Id



Graph Of Y Tan X Video Trigonometry Khan Academy



Geogebra Tutorial Functions



2




Solved Find Two Exact Values Of X In Degrees 0 X 360 Chegg Com




Evaluate Limit Gt 5x Cos X 3 Sin X 2 X 2 Tan 2x Brainly In



Www Thatonemathguy Com Uploads 7 0 1 3 Precalculus 2nd Edition Part 2 Pdf



Http Precalculus Flippedmath Com Uploads 1 1 3 0 Pc 10 4 Solutions Pdf



Trigonometry Archive April 04 21 Chegg Com




Explicit Function Which Is Tan X Pi 2 X Pi 2 Rotated By For Example 45 Degrees Anticlockwise About Origin Mathematics Stack Exchange
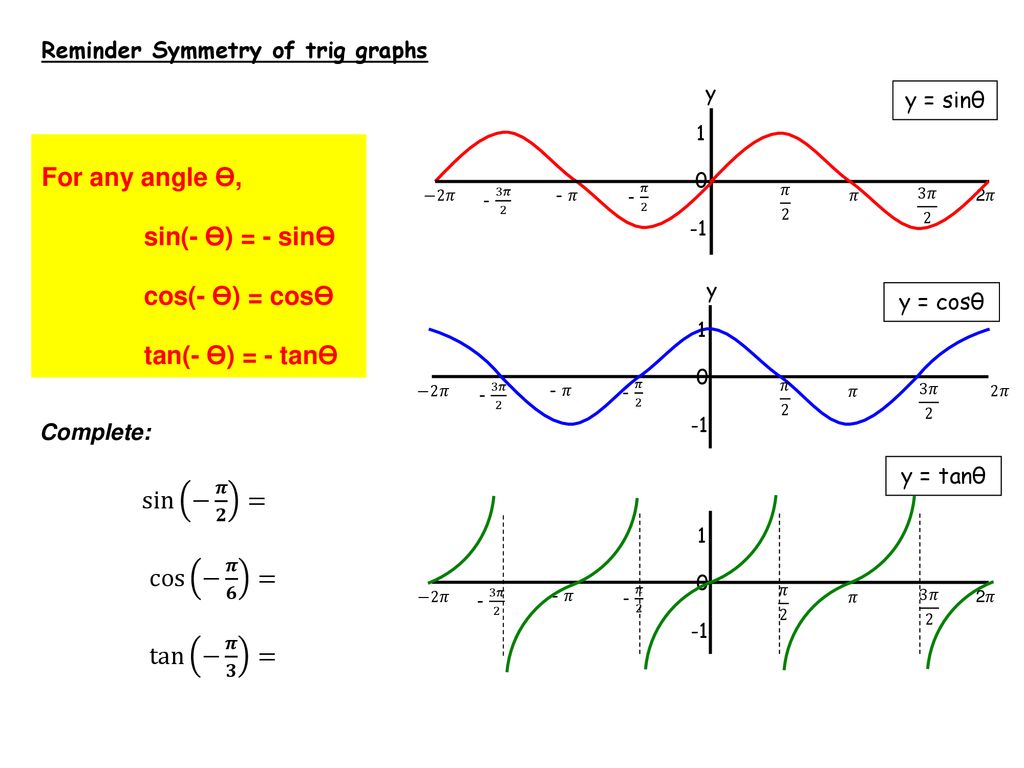



Trig Graphs And Equations Ppt Download
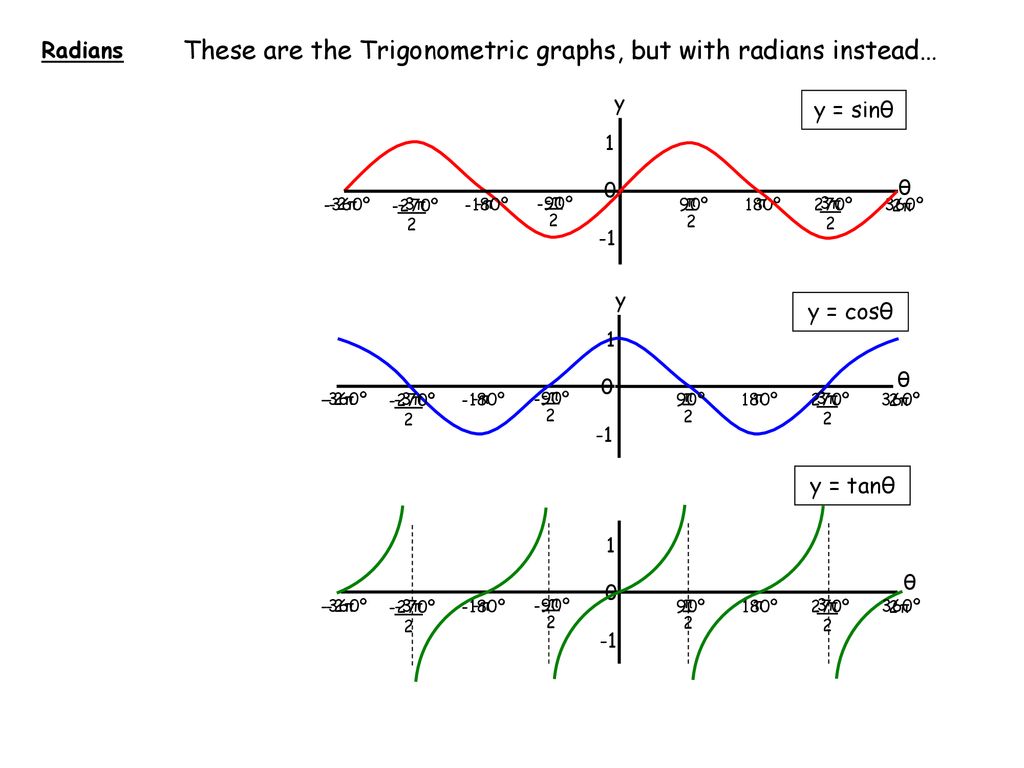



Trig Graphs And Equations Ppt Download




Trigonometric Functions Formulas Graphs Examples Faqs
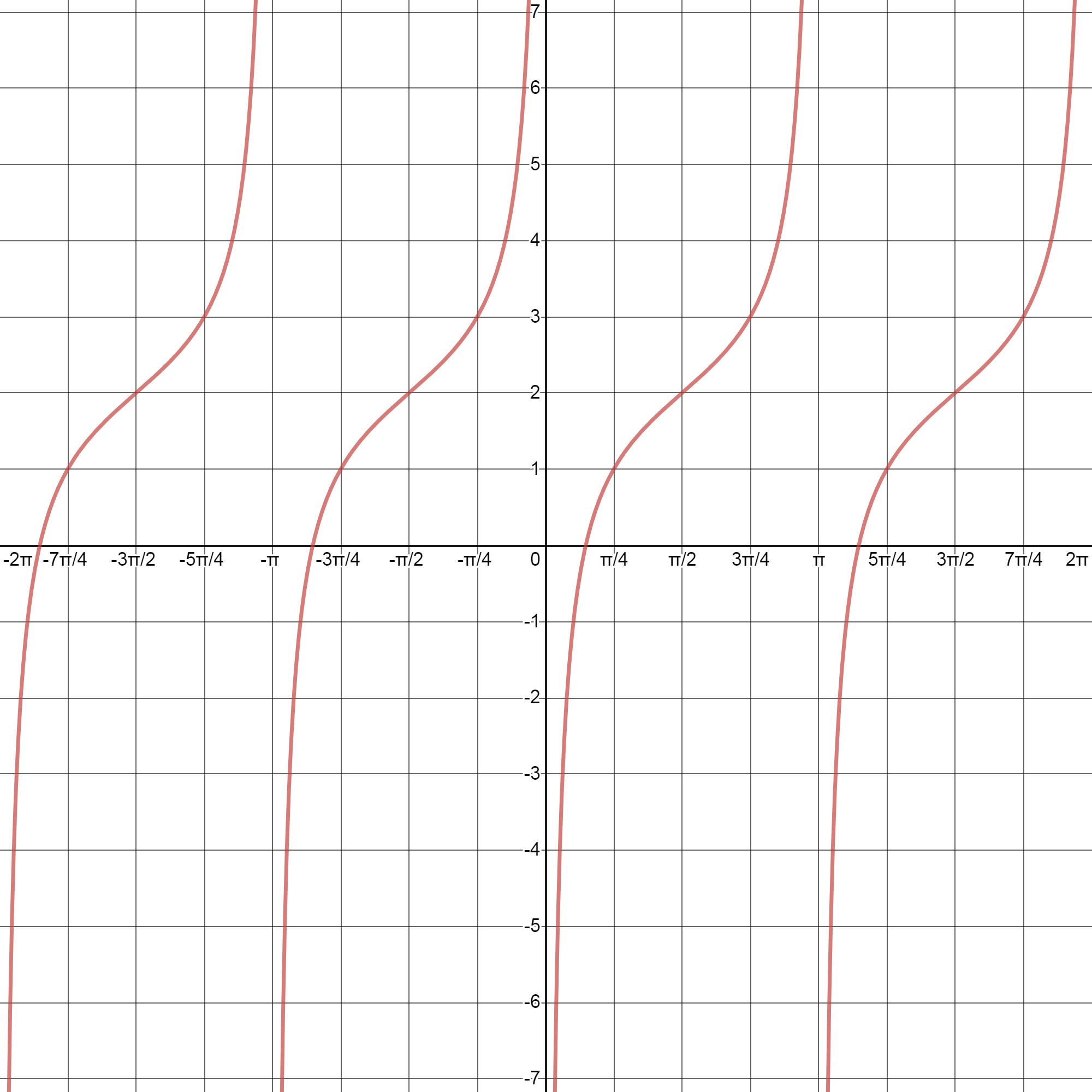



Trigonometry Quiz Quizizz
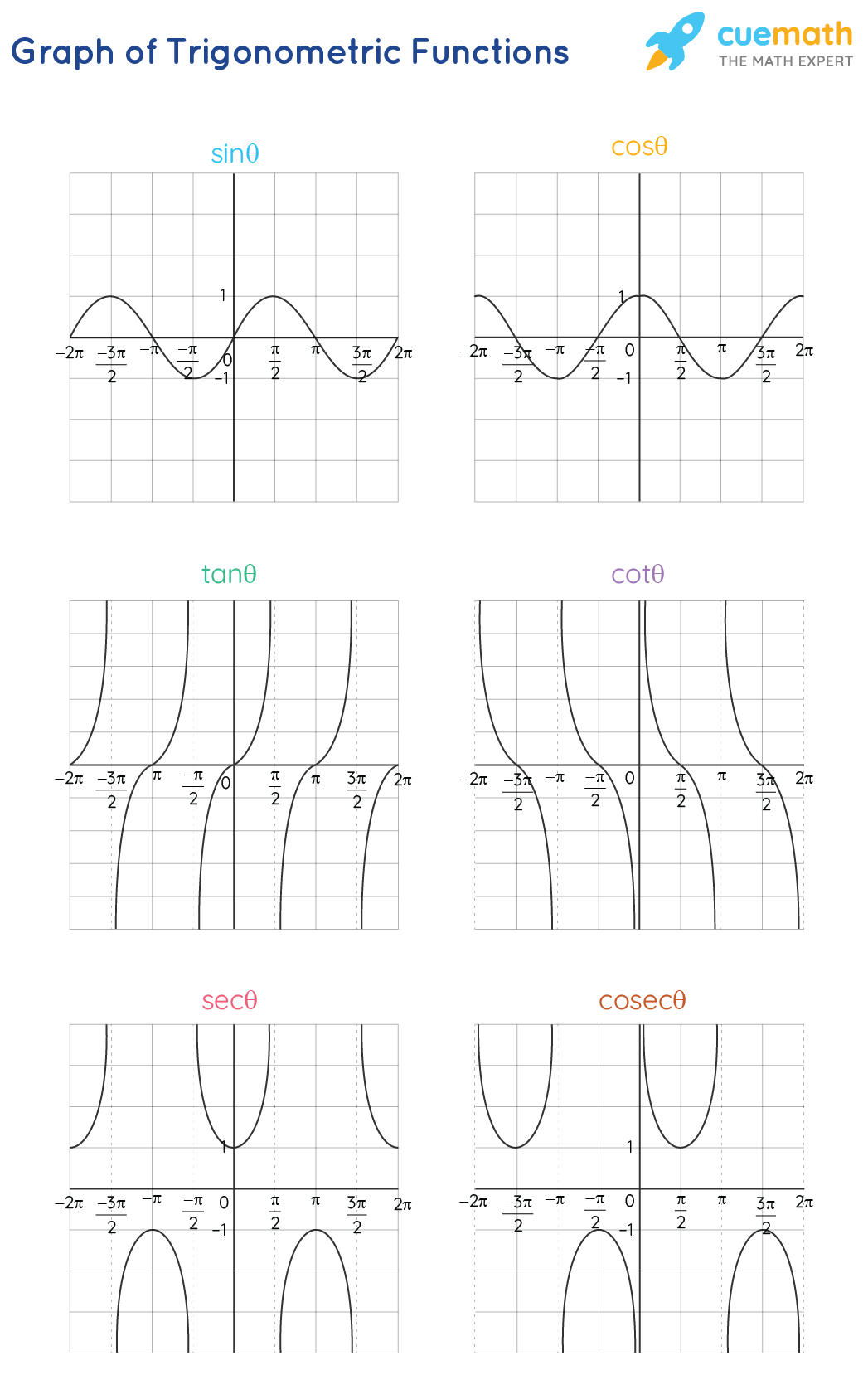



Trigonometric Functions Formulas Graphs Examples Faqs




Tangent And Cotangent Graphs Ck 12 Foundation
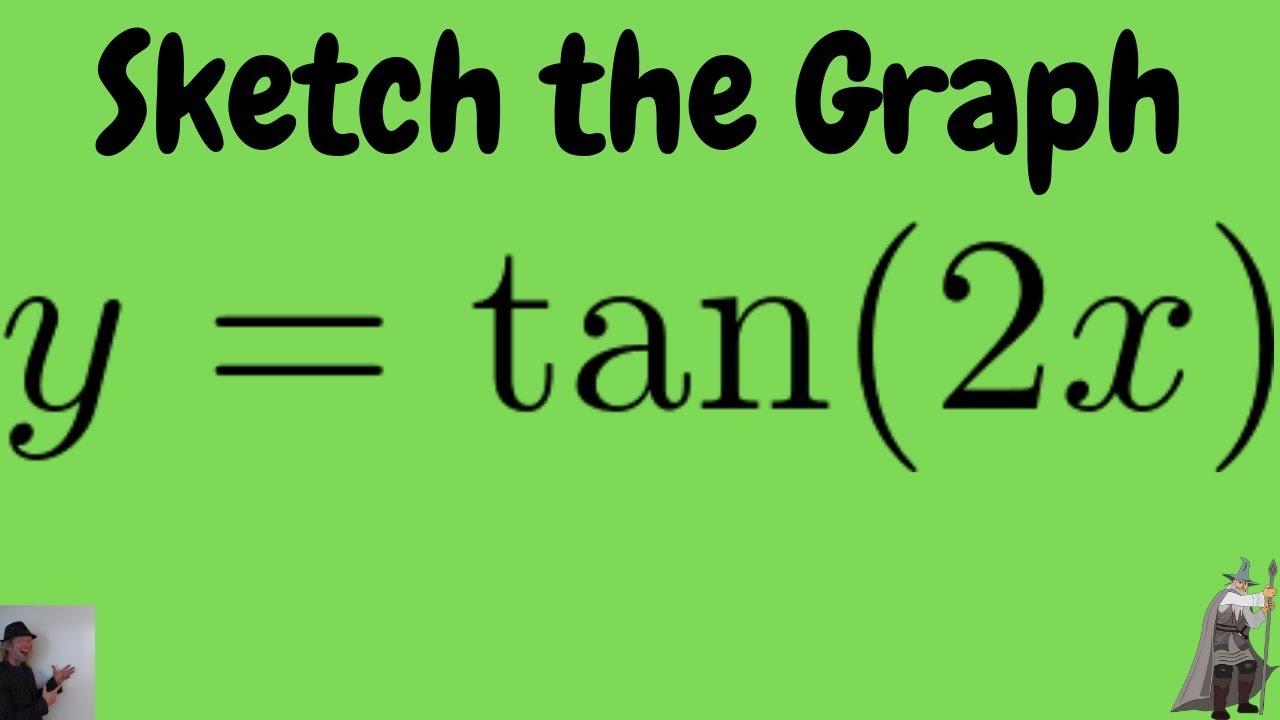



Sketch The Graph Of F X Tan 2x Youtube
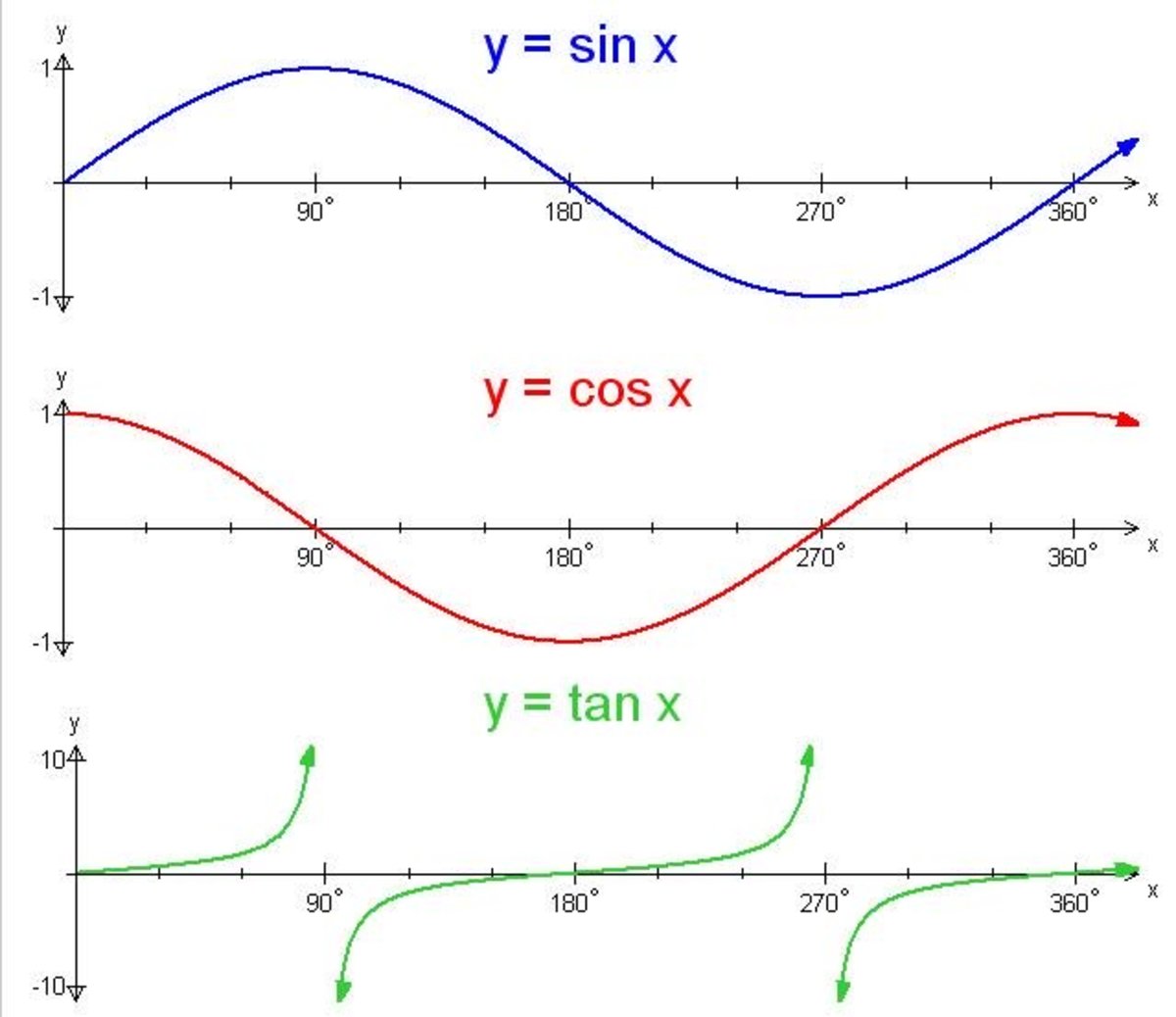



Trigonometry Graphing The Sine Cosine And Tangent Functions Owlcation
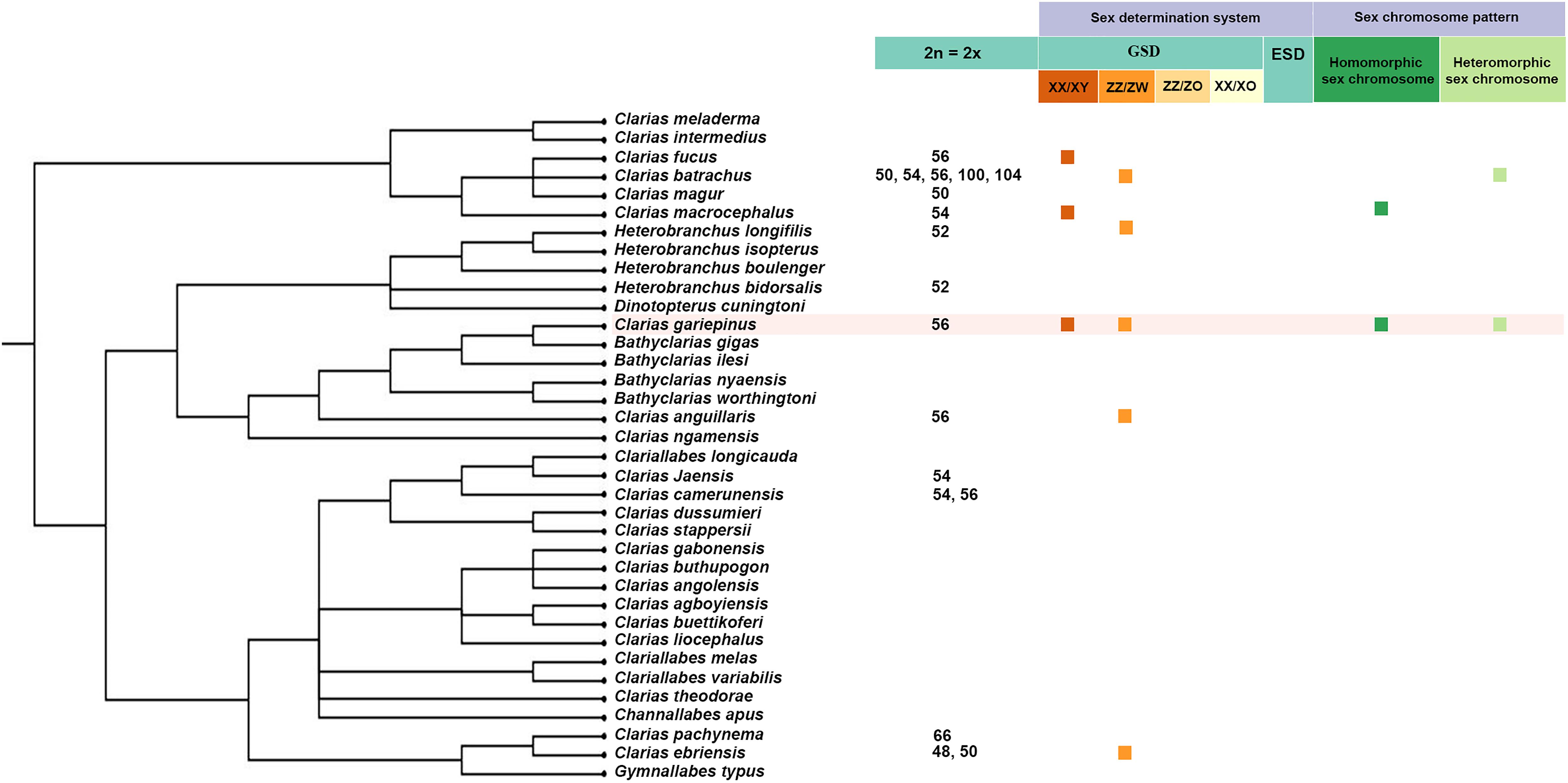



Frontiers An Investigation Of Zz Zw And Xx Xy Sex Determination Systems In North African Catfish Clarias Gariepinus Burchell 12 Genetics



1




New Senior Mathematics Extension 1 For Years 11 And 12 Pages 101 150 Flip Pdf Download Fliphtml5
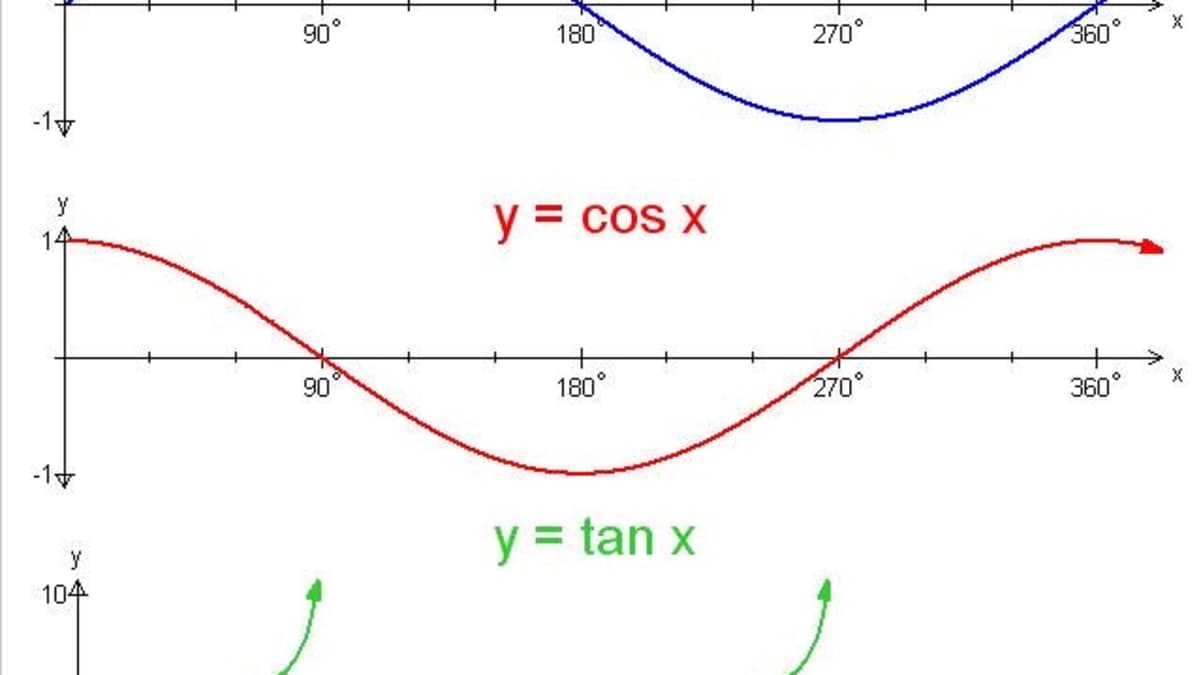



Trigonometry Graphing The Sine Cosine And Tangent Functions Owlcation




Trigonometric Functions Notes



Www Whiteplainspublicschools Org Cms Lib Ny Centricity Domain 360 Mr Ginos Trig Unit with toc Pdf




Section 5 4 More Trigonometric Graphs Graphs Of The Tangent Cotangent Secant And Cosecant Function Pdf Free Download
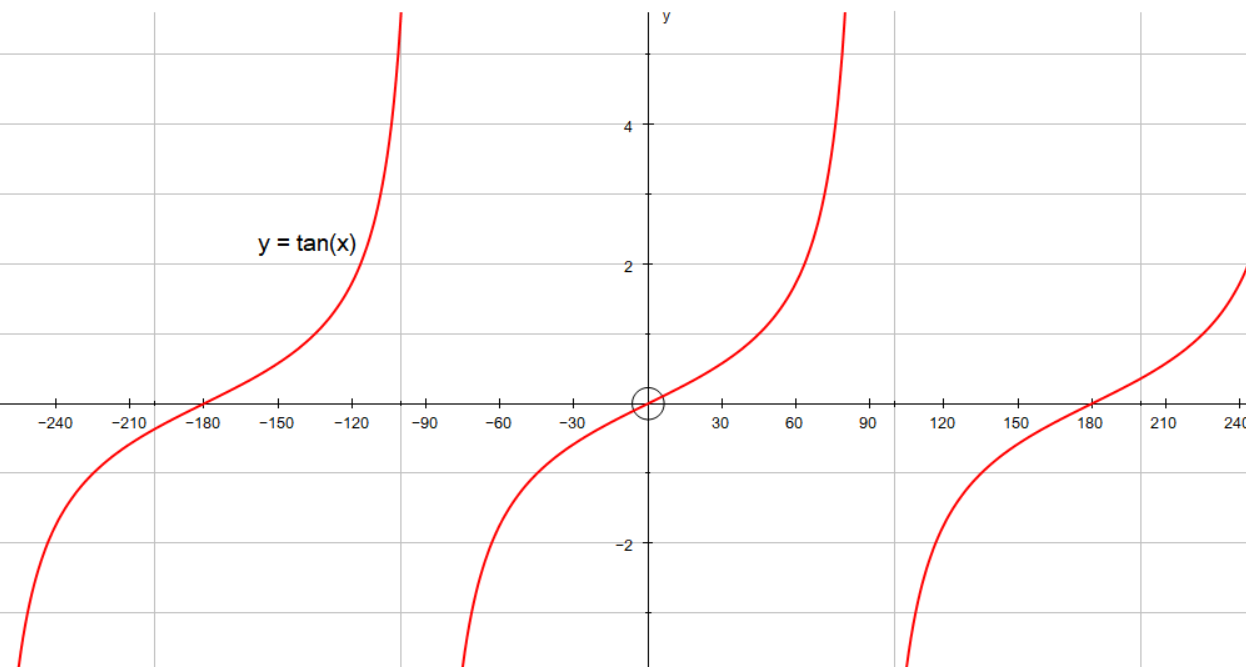



How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic




Sketching Y Tan 2x And Y Tan X 2 Youtube



Ms Unimelb Edu Au Data Assets Pdf File 0008 Basictrigonometric Functions Pdf
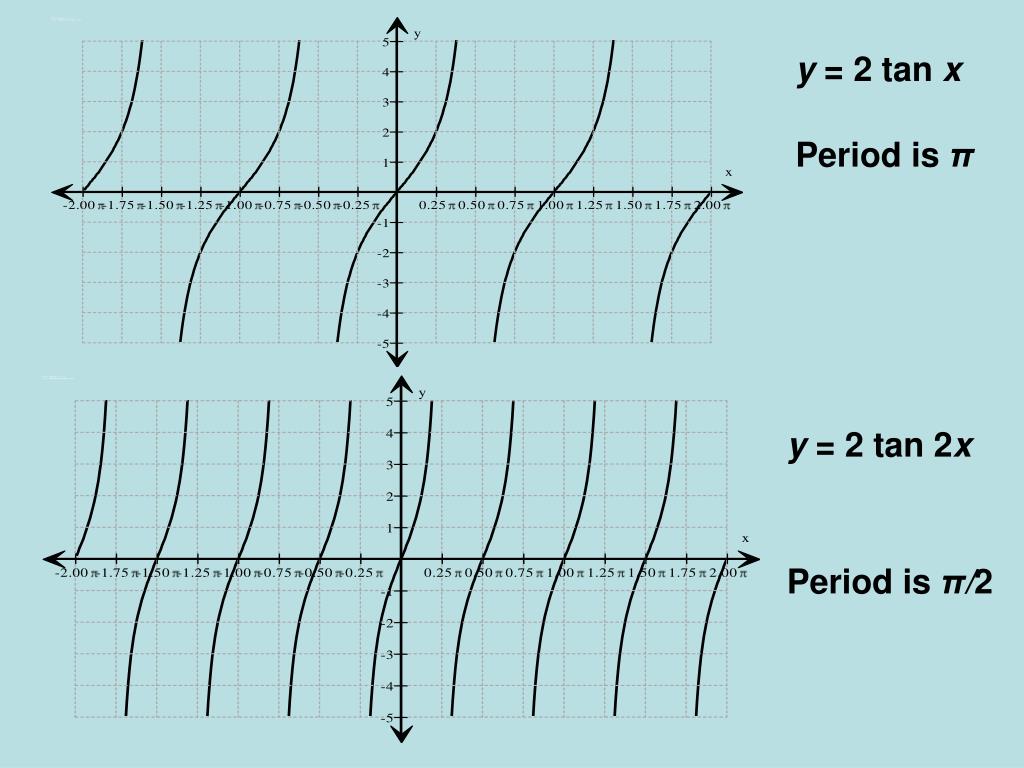



Ppt Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Powerpoint Presentation Id
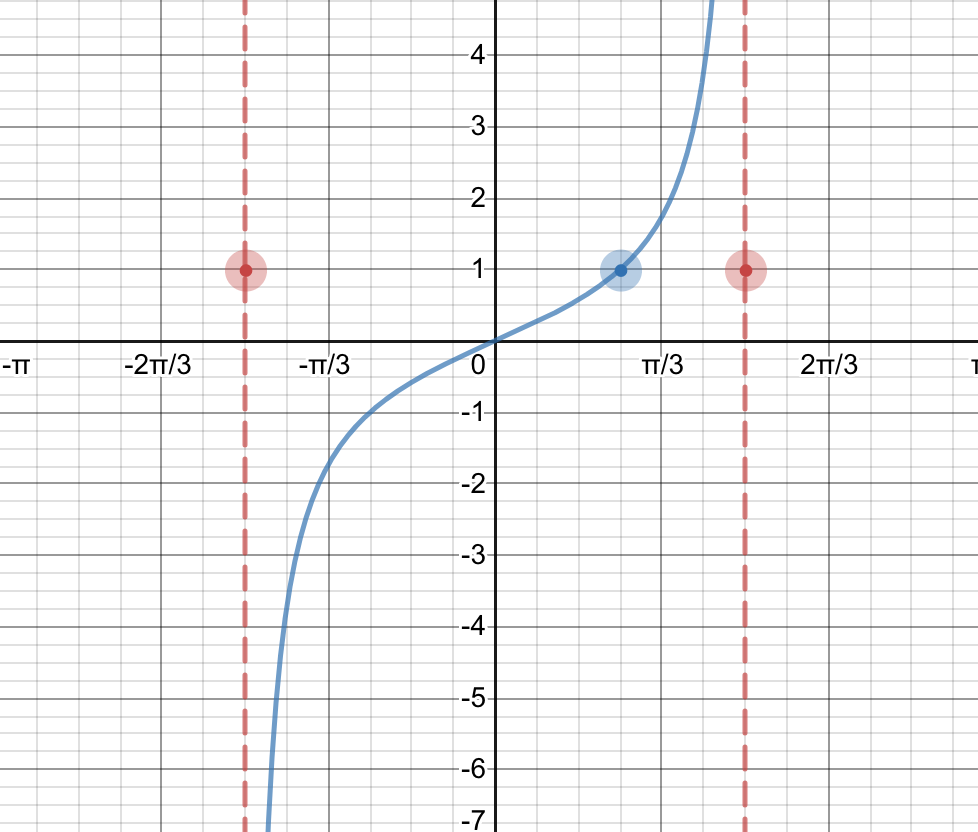



Answered Graph The Following Function Bartleby




4 5 Graphing Other Trig Functions Trickonometry




Howto How To Find Vertical Asymptotes Of Tan2x
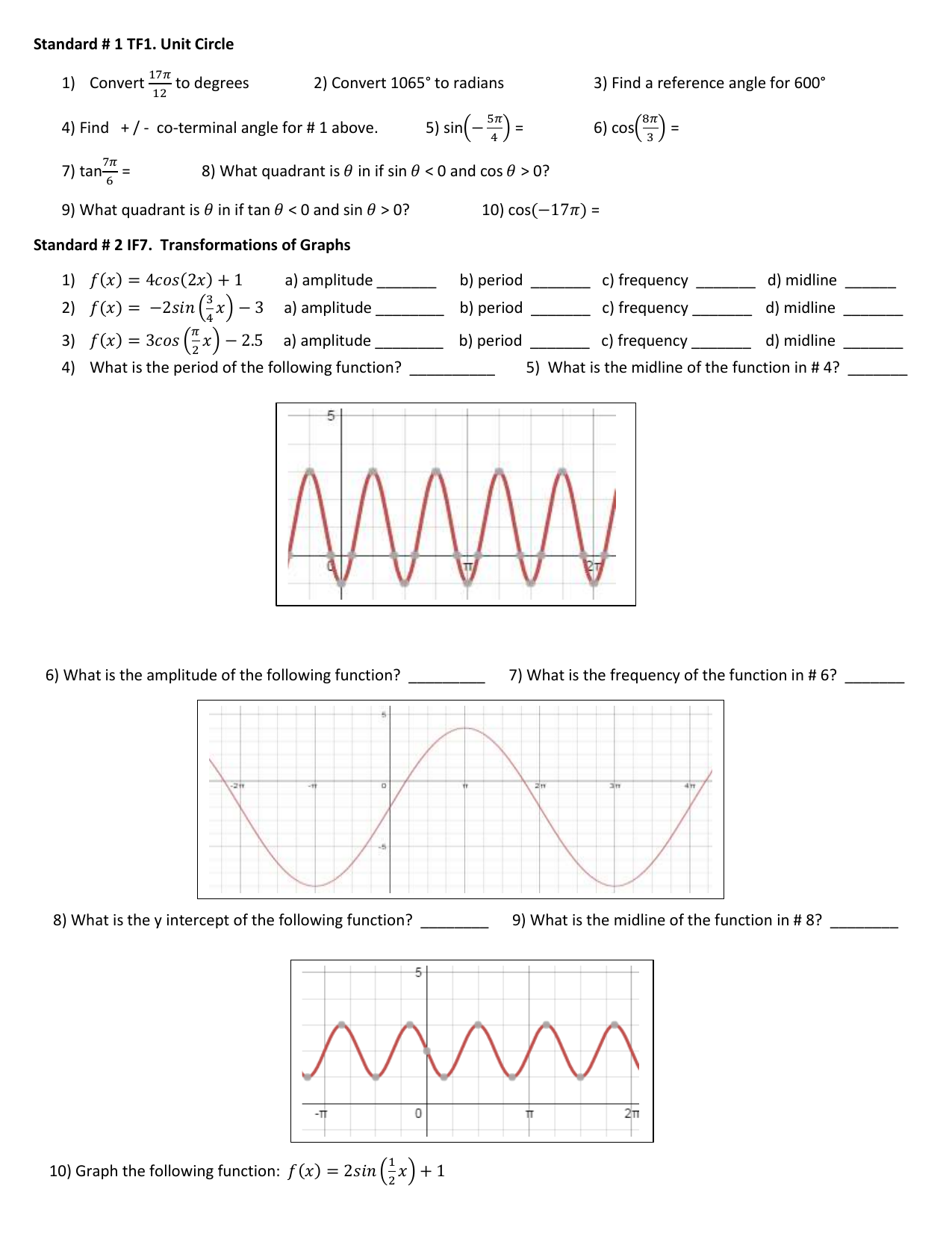



Standard 1 Tf1 Unit Circle Convert To Degrees 2 Convert 1065




C H A P T E R 4 Trigonometry Manualzz




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



Bestmaths
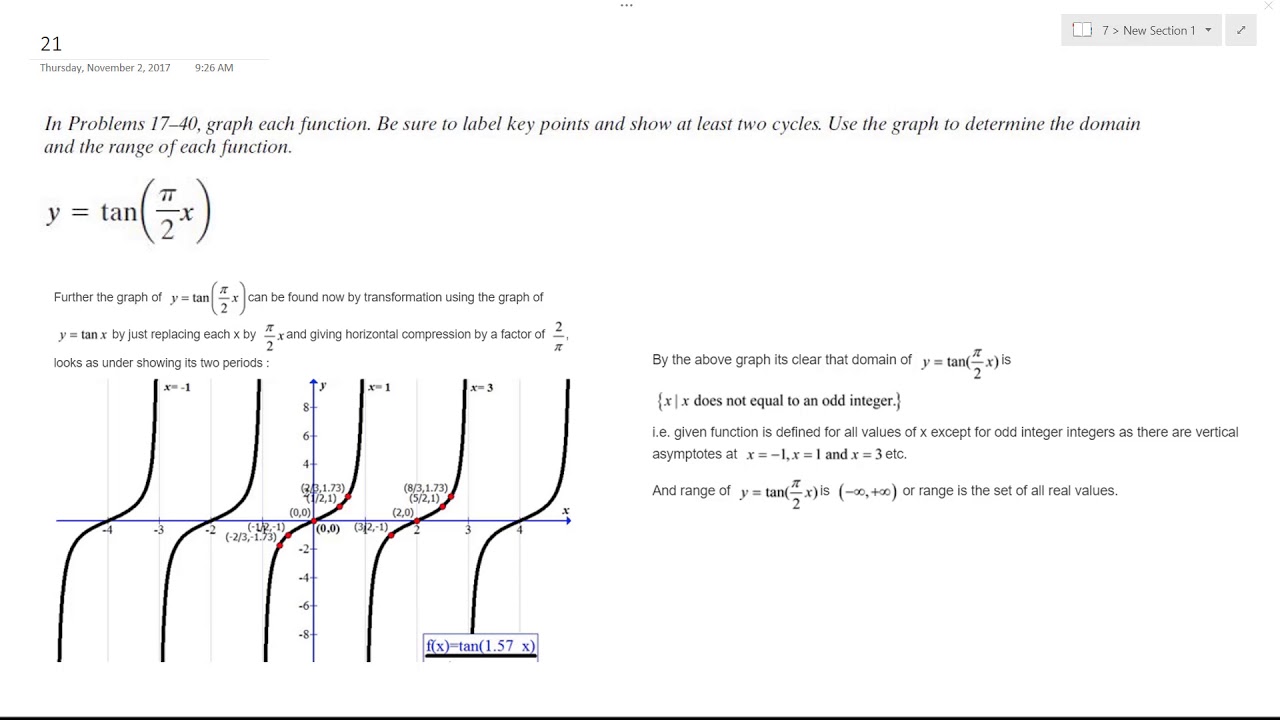



Y Tan Pi 2 X Graph And Label For 2 Cycles Youtube



1



Link Springer Com Content Pdf 10 1007 2f1 222 5 1 Pdf
.png)



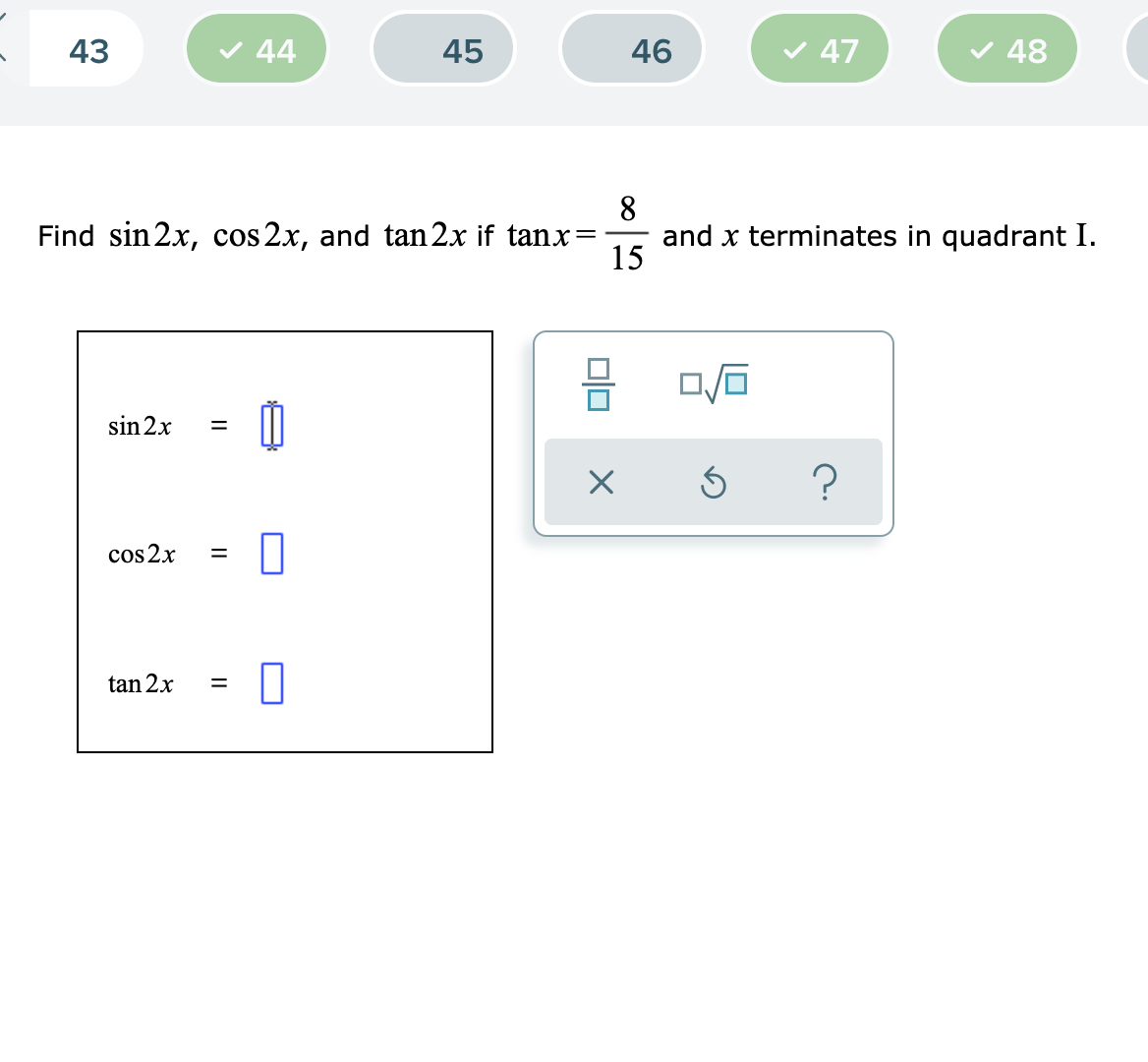
Find Sin2x Cos2x And Tan2x If Tanx 12 5 And X Terminates In Quadrant 1
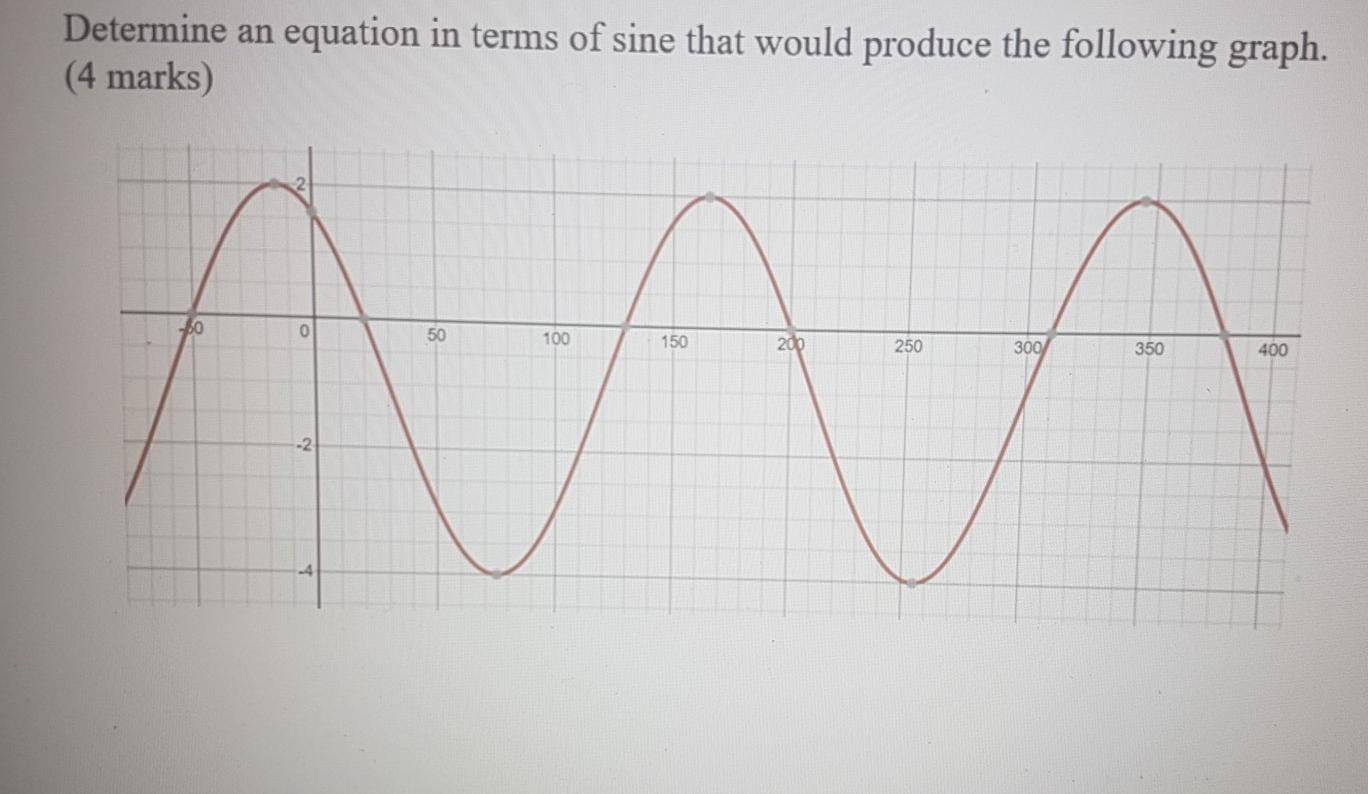



Trigonometry Archive January 27 21 Chegg Com



Http Www Sequoiahs Org Documents 1seqfix Ibmathhl Pdf
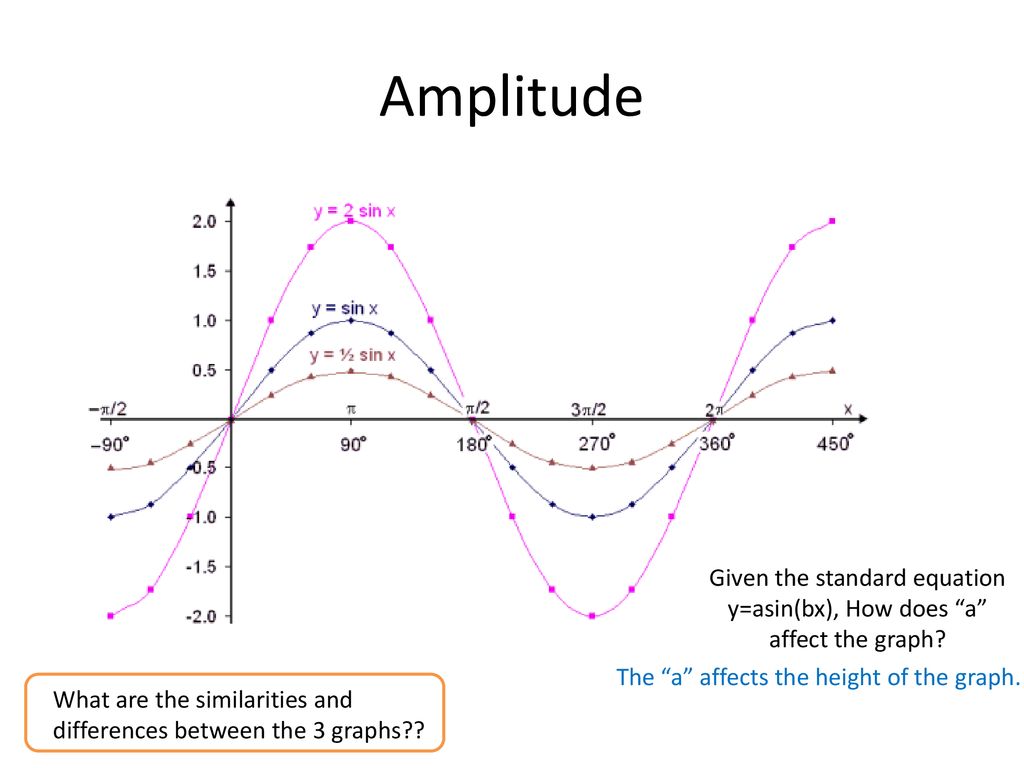



Graphs Of Trig Functions Ppt Download




If 1 K Tan 2x 4tanx 1 K 0 Has Real Roots Tanx 1 And Tanx 2 Then



2



Solved Sketch Two Periods Of The Graph Of The Functionh X 2sec 4 X 3 Identify The Stretching Factor Period And Asymptotes Course Hero



Azslide Com Download Solving Trigonometric Equations 5a30b0cdd08d6b5641a Html




Choose The Function Whose Graph Is Given By Brainly Com
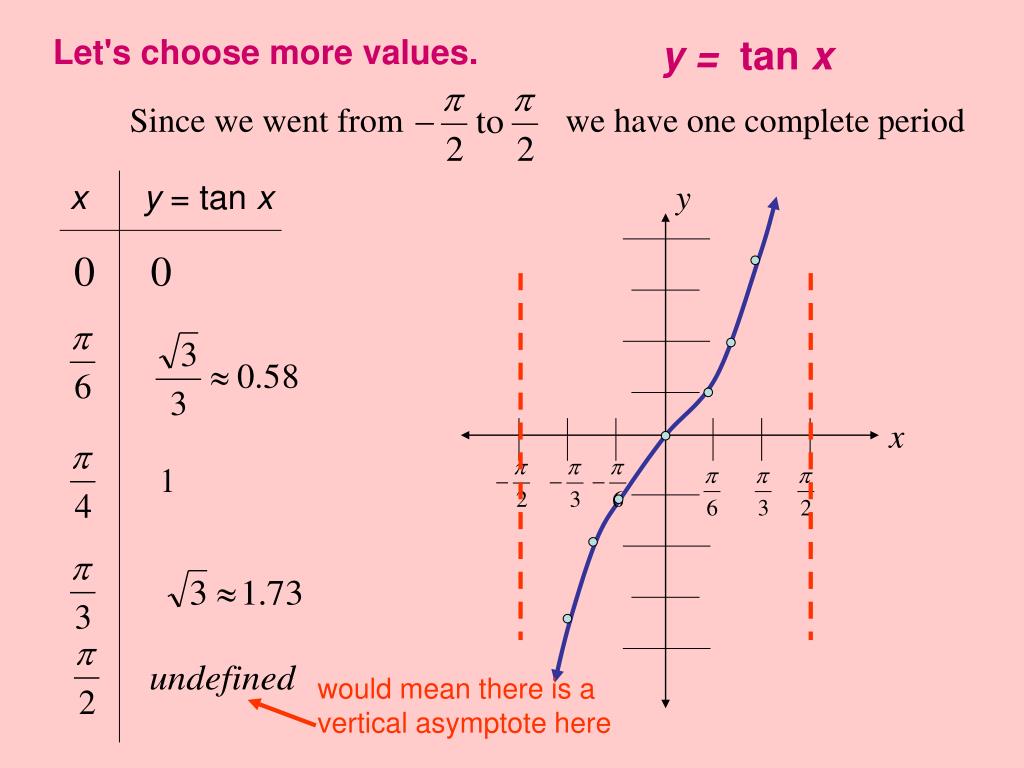



Ppt Graphs Of Other Trig Functions Powerpoint Presentation Free Download Id



2




New Senior Mathematics Extension 1 For Years 11 And 12 Pages 101 150 Flip Pdf Download Fliphtml5




Misscalcul8 April 16
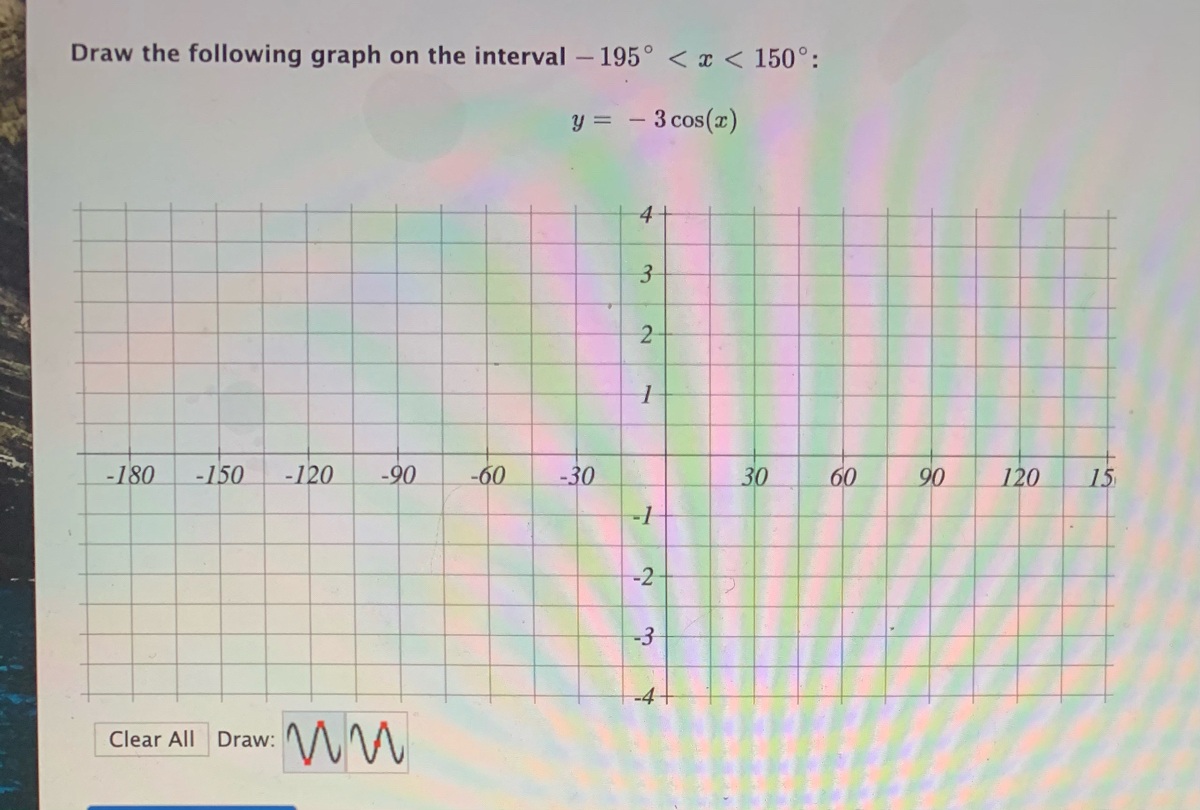



Answered Draw The Following Graph On The Bartleby



1
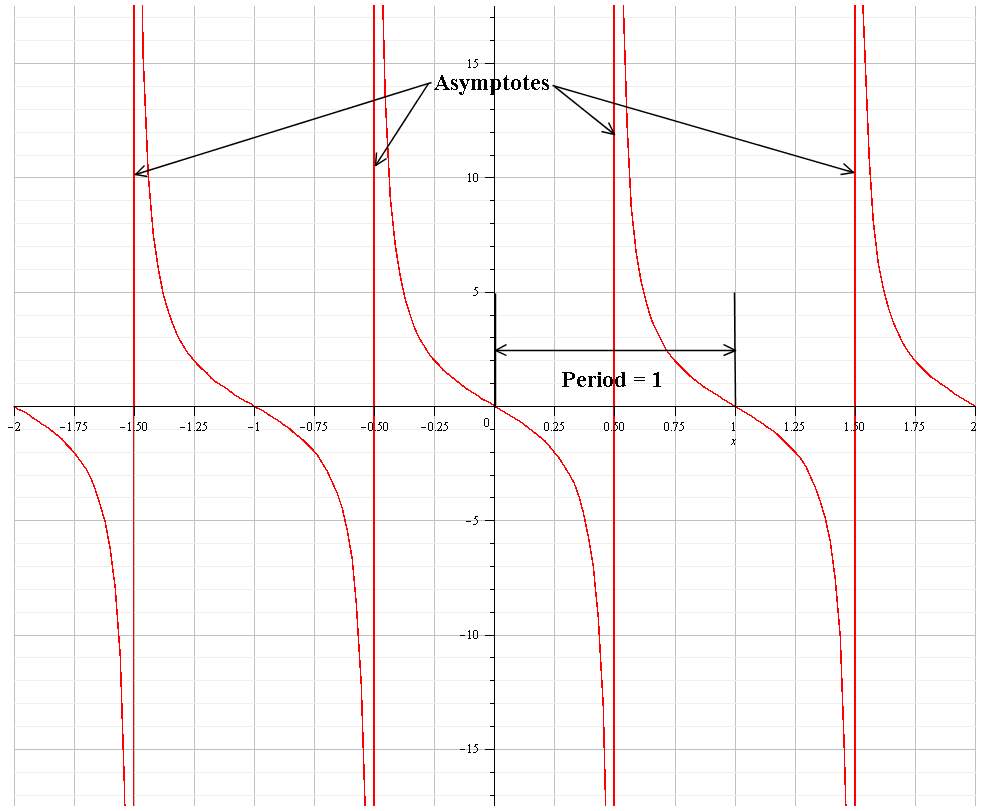



How Do You Identify The Period And Asympotes For Y 2tan Pitheta Socratic



How Can We Draw The Graph Of Tan X 2 Its Tan X Square And Not Tan Square X Quora
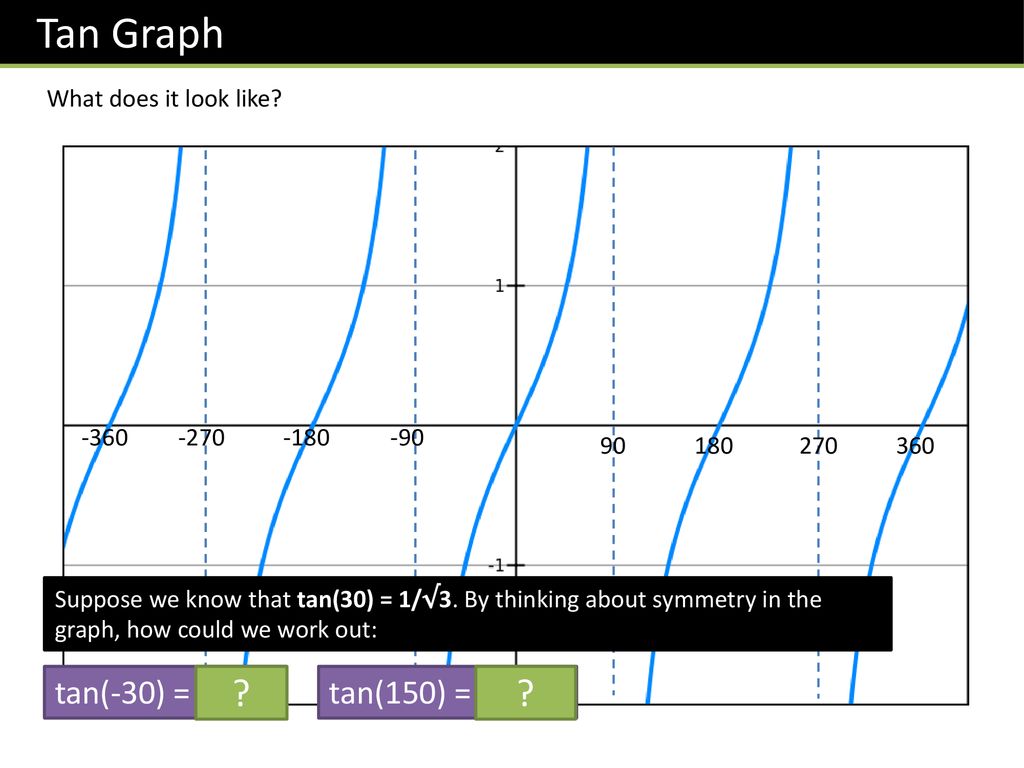



C1 Chapters 8 10 Trigonometry Ppt Download




18 G11 Math E Flip Book Pages 401 450 Pubhtml5
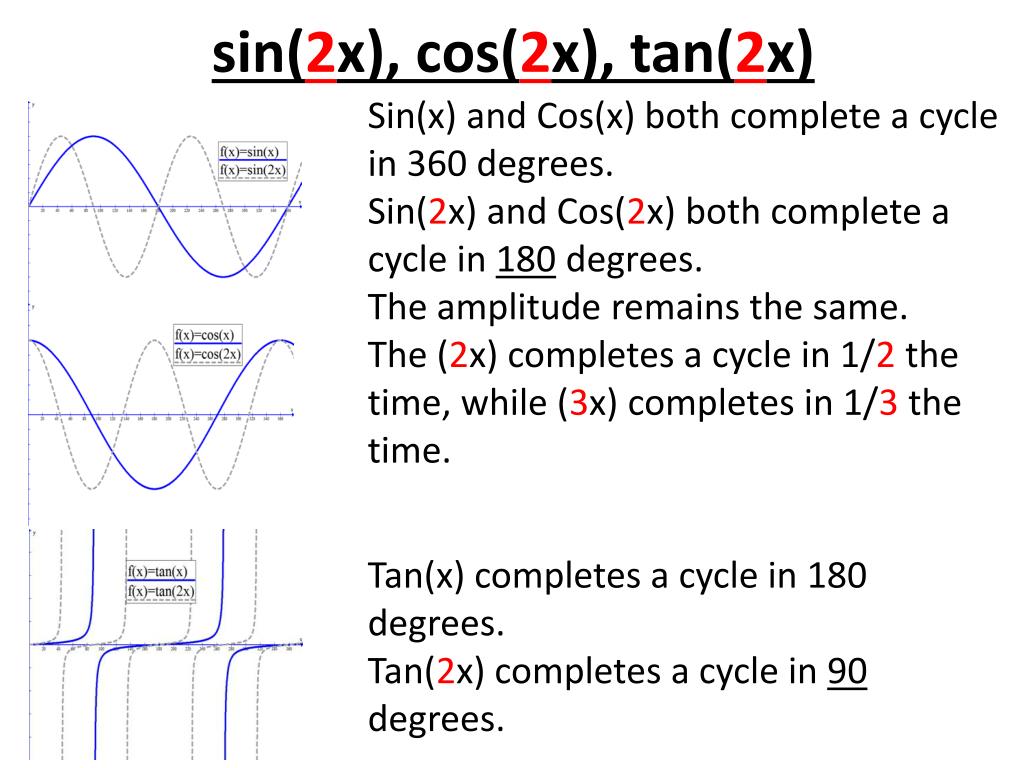



Ppt Trig Graphs Powerpoint Presentation Free Download Id



2




Gene Expression And Chromatin Accessibility During Progressive Emt And Met Linked To Dynamic Ctcf Engagement Biorxiv
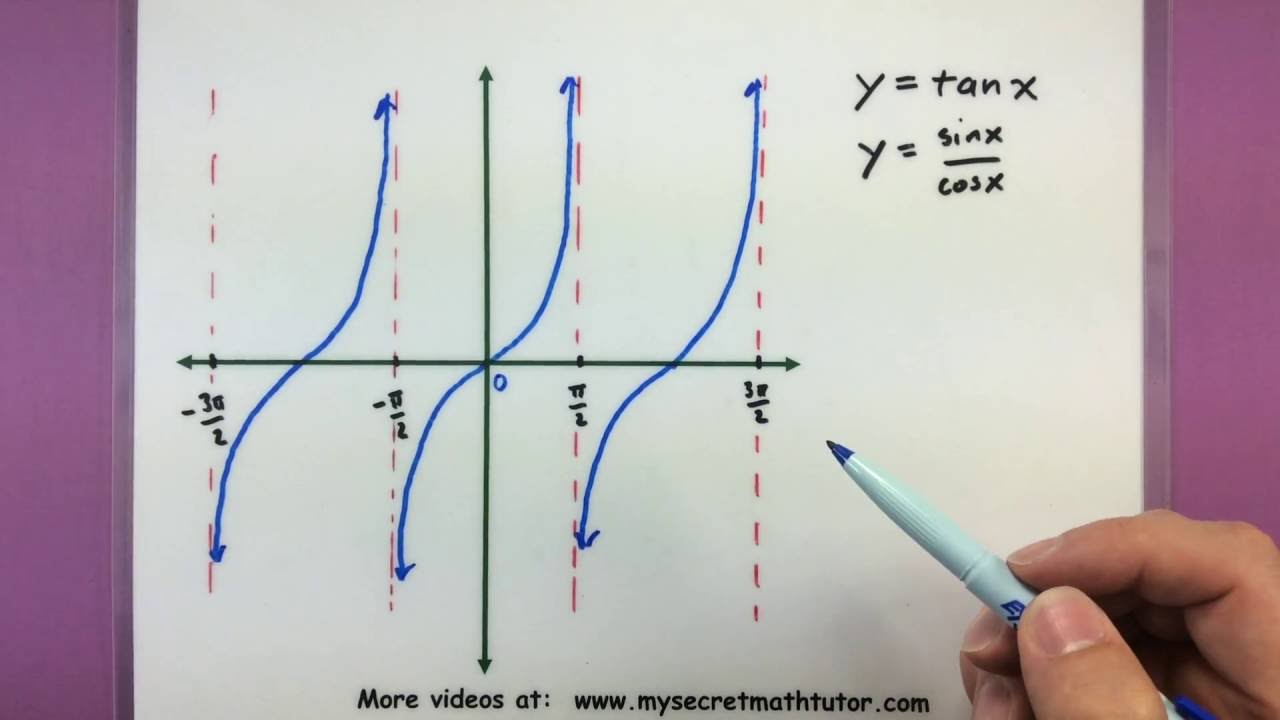



Trigonometry The Graphs Of Tan And Cot Youtube
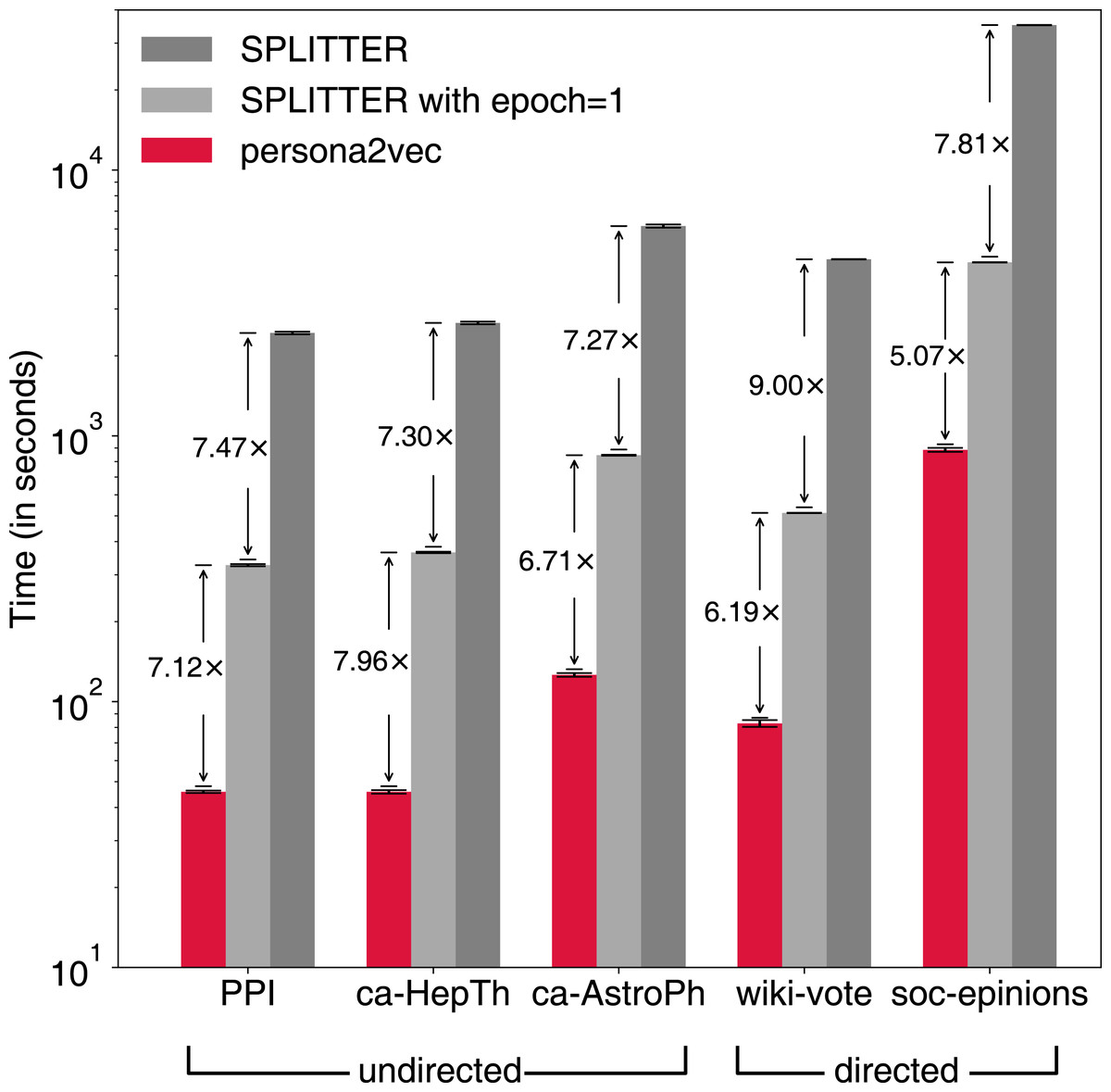



Persona2vec A Flexible Multi Role Representations Learning Framework For Graphs Peerj




Explicit Function Which Is Tan X Pi 2 X Pi 2 Rotated By For Example 45 Degrees Anticlockwise About Origin Mathematics Stack Exchange
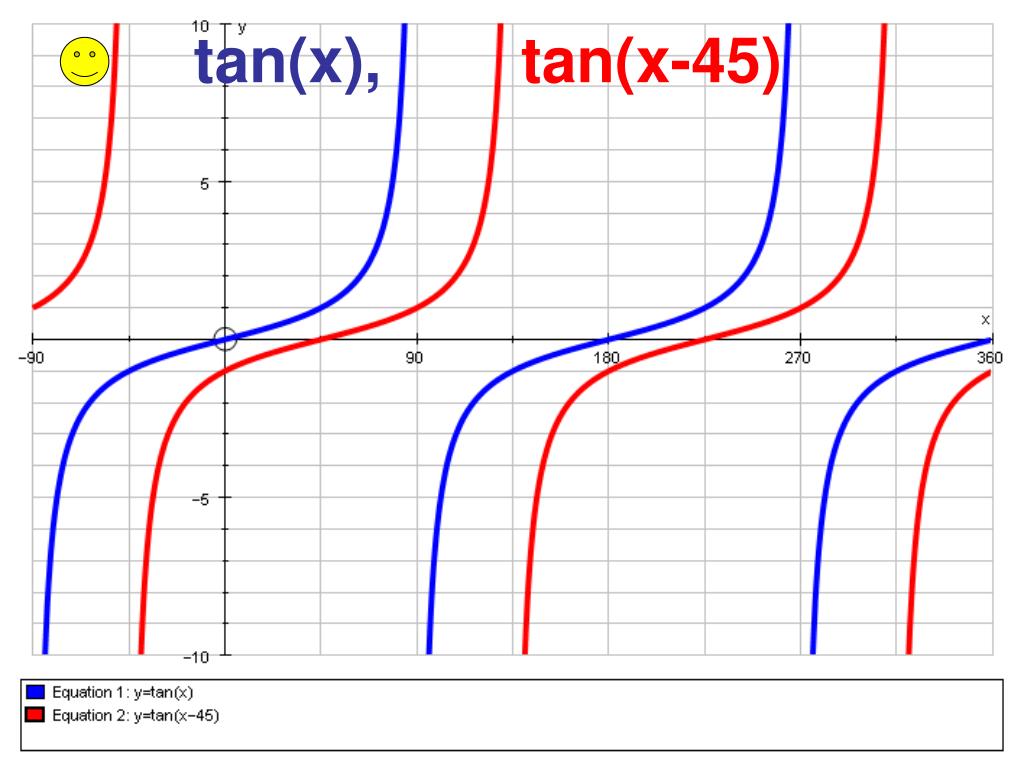



Ppt Translations And Transformations Of Trigonometric Functions Powerpoint Presentation Id
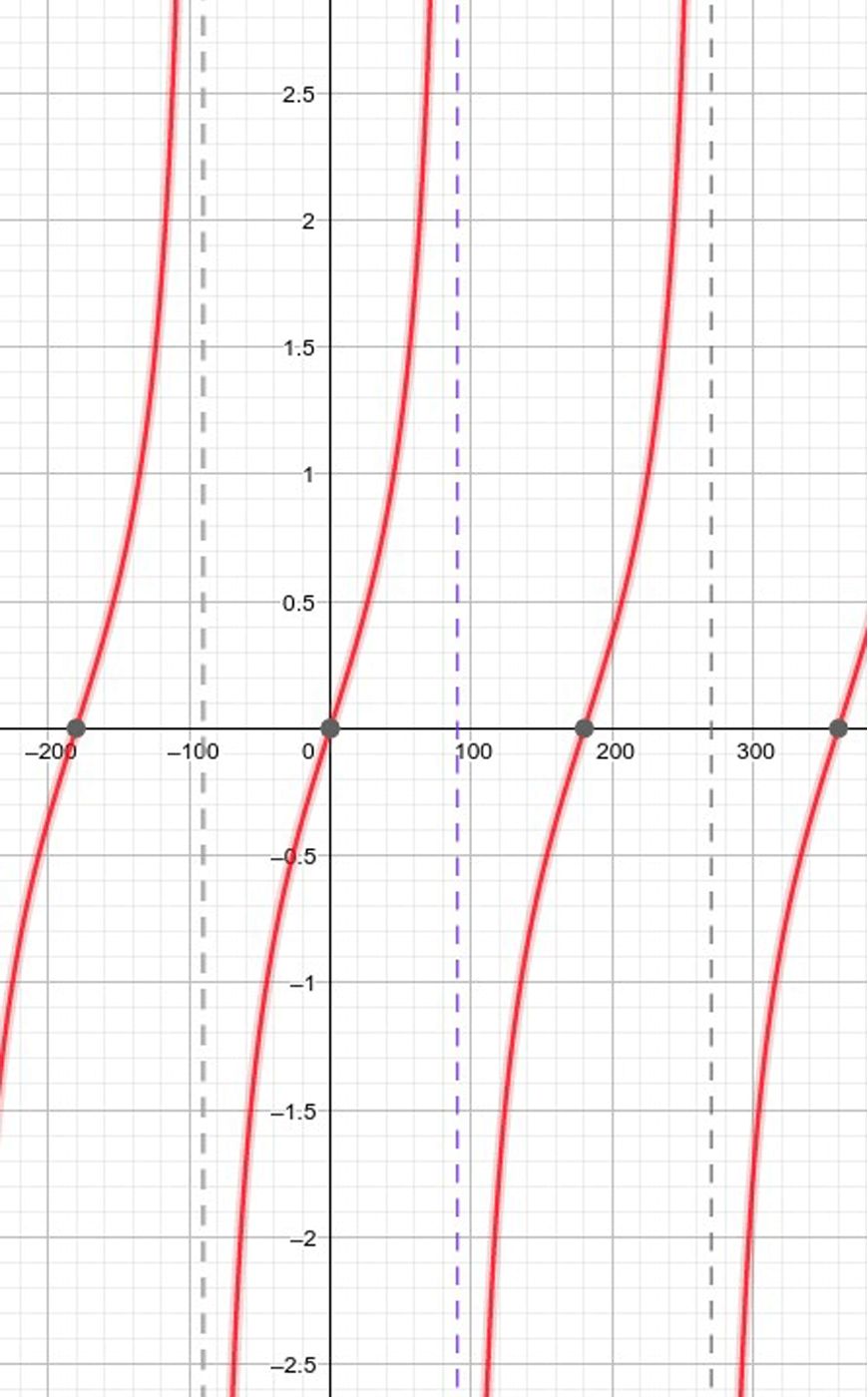



Part 4 Year 10 Further Trigonometry Applications Year 10 Maths Guide



Http Jennanolan Weebly Com Uploads 1 0 7 1 Lesson6key Pdf



Answered 43 V 44 45 46 V 47 V 48 8 And X Bartleby



Http Www Jessamine K12 Ky Us Userfiles 1044 Classes Key to trig practice test part 2 Pdf Id



By Siby Sebastian Pgt Maths Ppt Download




Cos X Y Formula Cienaigh
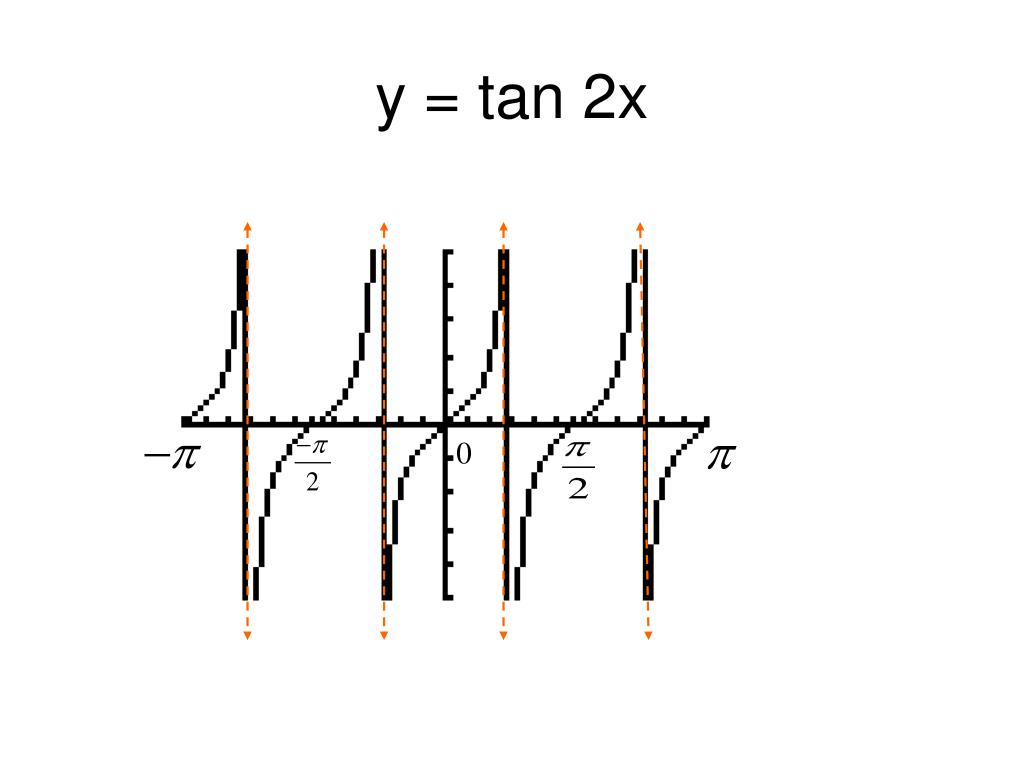



Tan2x ただの悪魔の画像



Solved Graph F X 1 2 Cos Theta 150 Where Are The Minimums X Coordinates Course Hero


